Pile Capacity with Pile-Driving Formulas

Pile-driving formulas

Intuitively, we would expect piles that are difficult to drive (i.e., those with a high blow count) will have a greater downward load capacity than those that drive more easily. Thus, there should be some correlation between blow count and load capacity. Engineers have attempted to define this relationship by developing empirical correlations between hammer weight, blow count, and the static load capacity. These relationships are collectively known as pile-driving formulas. These equations are widely used in the field to determine whether a pile has reached a satisfactory bearing value at the predetermined depth.

Dozens of pile-driving formulas have been proposed over the years. One of the earliest such expressions, commonly referred to as the Engineering News Record (ENR) formula, is stated as

$\displaystyle {{Q}_{u}}=\frac{{{{W}_{R}}h}}{{S+C}}$

where $\displaystyle {{Q}_{u}}$ is the ultimate load, $\displaystyle {{W}_{R}}$ is the weight of the ram, $\displaystyle h$ is the height of fall of the ram, $\displaystyle S$ is the penetration of pile per hammer blow, and $\displaystyle C$ is a constant. The pile penetration, $\displaystyle S$ , is usually based on the average value obtained from the last few driving blows. In the equation’s original form, the values of $\displaystyle C$ recommended were 1 in. (25.4 mm) for drop hammers and 0.1 in. (2.54 mm) for steam hammers. A factor of safety of 6 was recommended for estimating allowable bearing capacity. Note that, for single- and double-acting hammers, the term $\displaystyle {{W}_{R}}h$ can be replaced with $\displaystyle \eta {{H}_{E}}$ , where $\displaystyle \eta$ is the efficiency of the hammer and $\displaystyle {{H}_{E}}$ is the rated energy of the hammer, giving

$\displaystyle {{Q}_{u}}=\frac{{\eta {{H}_{E}}}}{{S+C}}$

The ENR equation was developed for timber piles using drop hammers for installation but has since been (somewhat unduly) used to estimate or check the ultimate load capacity of all types of piles. A modified, more recent form of the ENR formula is

$\displaystyle {{Q}_{u}}=\frac{{\eta {{W}_{R}}h}}{{S+C}}\left( {\frac{{{{W}_{R}}+{{n}^{2}}{{W}_{P}}}}{{{{W}_{R}}+{{W}_{P}}}}} \right)$

where $\displaystyle {{W}_{P}}$ is the weight of the pile + cap and $\displaystyle n$ is the coefficient of restitution between the ram and the pile cap. Some typical values of hammer efficiency and coefficient of restitution are listed below.

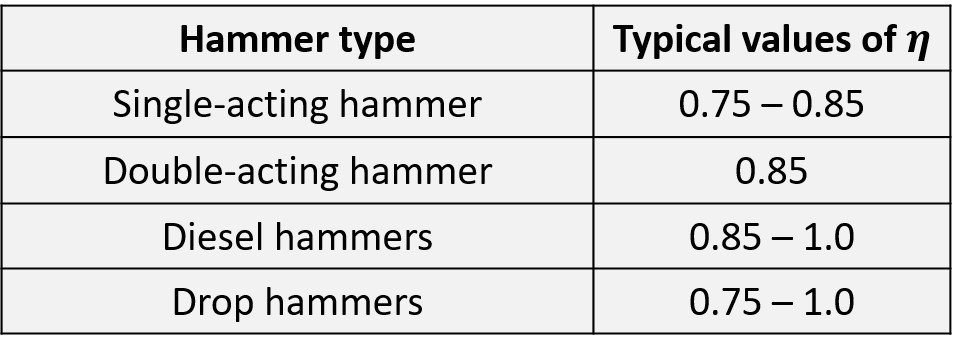
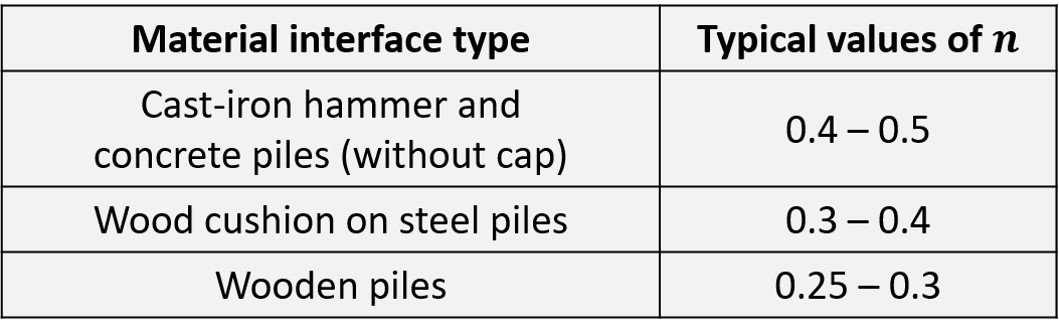
Another expression, the Danish formula, was proposed in 1967,

$\displaystyle {{Q}_{u}}=\frac{{\eta {{H}_{E}}}}{{S+\sqrt{{\frac{{\eta {{H}_{E}}L}}{{2{{A}_{p}}{{E}_{p}}}}}}}}$

where $\displaystyle L$ is the length of the pile, $\displaystyle {{E}_{p}}$ is the modulus of elasticity of the pile material, and $\displaystyle {{A}_{p}}$ is the cross-sectional area of the pile.

A fourth valuable expression, proposed by Janbu in 1953, is

$\displaystyle {{Q}_{u}}=\frac{{\eta {{H}_{E}}}}{{{K}'S}}$

where

$\displaystyle {K}'={{C}_{d}}\left( {1+\sqrt{{1+\frac{{{\lambda }'}}{{{{C}_{d}}}}}}} \right)$

with

$\displaystyle {{C}_{d}}=0.75+0.14\left( {\frac{{{{W}_{p}}}}{{{{W}_{R}}}}} \right)$

$\displaystyle {\lambda }'=\frac{{\eta {{H}_{E}}L}}{{{{A}_{p}}{{E}_{p}}{{S}^{2}}}}$

The engineer can compare the estimated ultimate pile load capacity with that calculated from the pile driving formulas. The reliability of the pile driving formulas is difficult to ascertain. Experience is required to make a decision on whether to rely on the pile loading capacity from the pile-driving formulas or other methods of pile foundation analysis. Having introduced some pile-driving formulas, we now present a simple calculation example.

Example

A square pile with cross-sectional area of 30 in.² and weight 9 kip is driven by a hammer. The maximum rated hammer energy is 40 kip-ft, the weight of the ram is 12 kip, and the length of the pile is 90 ft. Also, we have coefficient of restitution = 0.35, weight of the pile cap = 2.4 kip, hammer efficiency = 0.85, and number of blows for the last inch of penetration = 10. The modulus of elasticity of the pile steel is $\displaystyle 30\times {{10}^{6}}$ lb/in.²

A) Estimate the pile capacity using the basic ENR formula. Use FS = 6.

B) Estimate the pile capacity using the modified ENR formula. Use FS = 4.

C) Estimate the pile capacity using the Danish formula. Use FS = 8.

D) Estimate the pile capacity using Janbu’s formula. Use FS = 6.

A) The hammer energy is converted as $\displaystyle {{H}_{E}}$ = 40 $\displaystyle \times$ 12 = 480 kip-in. Appealing to the ENR formula, we have

$\displaystyle {{Q}_{u}}=\frac{{\eta {{H}_{E}}}}{{S+C}}=\frac{{0.85\times 480}}{{{1}/{{10}}\;+0.1}}=2040\,\ \text{kip}$

Applying the factor of safety gives

$\displaystyle {{Q}_{{\text{all}}}}=\frac{{2040}}{6}=340\,\,\text{kip}\leftarrow$

B) The weight of the pile + cap ensemble is $\displaystyle {{W}_{p}}$ = 9 + 2.4 = 11.4 kip. Applying the modified ENR formula brings to

$\displaystyle {{Q}_{u}}=\frac{{\eta {{W}_{R}}h}}{{S+C}}\left( {\frac{{{{W}_{R}}+{{n}^{2}}{{W}_{P}}}}{{{{W}_{R}}+{{W}_{P}}}}} \right)$

$\displaystyle \therefore {{Q}_{u}}=\frac{{0.85\times 480}}{{{1}/{{10}}\;+0.1}}\left( {\frac{{12+{{{0.35}}^{2}}\times 11.4}}{{12+11.4}}} \right)=1170\,\,\text{kip}$

Applying the factor of safety gives

$\displaystyle {{Q}_{{\text{all}}}}=\frac{{1170}}{4}=293\,\,\text{kip}\leftarrow$

C) Before applying the Danish formula, we compute the term

$\displaystyle \sqrt{{\frac{{\eta {{H}_{E}}L}}{{2{{A}_{p}}{{E}_{p}}}}}}=\sqrt{{\frac{{0.85\times 480\times \left( {90\times 12} \right)}}{{2\times 30\times \left( {30\times {{{10}}^{6}}} \right)}}}}=0.0156$

so that

$\displaystyle {{Q}_{u}}=\frac{{0.85\times \left( {40\times 12} \right)}}{{0.1+0.0156}}=3530\ \text{kip}$

Applying the factor of safety gives

$\displaystyle {{Q}_{{\text{all}}}}=\frac{{3530}}{8}=441\,\,\text{kip}\leftarrow$

D) We must first determine parameters $\displaystyle {{C}_{d}}$ and $\displaystyle {\lambda }'$ ,

$\displaystyle {{C}_{d}}=0.75+0.14\left( {\frac{{{{W}_{p}}}}{{{{W}_{R}}}}} \right)=0.75+0.14\times \frac{{11.4}}{{12}}=0.883$

$\displaystyle {\lambda }'=\left( {\frac{{\eta {{H}_{E}}L}}{{{{A}_{p}}{{E}_{p}}{{S}^{2}}}}} \right)=\left[ {\frac{{0.85\times 480\times \left( {90\times 12} \right)}}{{30\times \left( {30\times {{{10}}^{6}}} \right)\times {{{0.1}}^{2}}}}} \right]=0.049$

so that

$\displaystyle {K}'={{C}_{d}}\left( {1+\sqrt{{1+\frac{{{\lambda }'}}{{{{C}_{d}}}}}}} \right)=0.883\left( {1+\sqrt{{1+\frac{{0.049}}{{0.883}}}}} \right)=1.79$

and

$\displaystyle {{Q}_{u}}=\frac{{\eta {{H}_{E}}}}{{{K}'S}}=\frac{{0.85\times 480}}{{1.79\times 0.1}}=2280\,\,\text{kip}$

Lastly, we apply the factor of safety to obtain

$\displaystyle {{Q}_{{\text{all}}}}=\frac{{2280}}{6}=380\,\,\text{kip}\leftarrow$

Limitations

As can be seen from the example above, the ultimate loads calculated by each formula can vary by a wide margin. Our most conservative result – an ultimate load of 1170 kip, obtained with the modified ENR formula – deviates from the most daring result – a $\displaystyle {{Q}_{u}}$ of 3530 kip, obtained with the Danish formula – by 200 percent. The factors of safety were deliberately chosen to make the results closer to each other, but this is a mathematical convenience that the practicing engineer cannot afford. The pile-driving formulas are inherently innacurate. In a 1942 article, Peck suggested marking various pile capacities on a set of poker chips, selecting a chip at random, and using that capacity for design; his data suggested that even this method would be more accurate than employing pile-driving formulas. Nevertheless, analyses of this type have been used in engineering practice for decades and remain a historically important approach to pile analysis.

References

• BUDHU, M. (2011). Soil Mechanics and Foundations. 3rd edition. Hoboken: John Wiley and Sons.

• CODUTO, D. (2001). Foundation Design: Principles and Practices. 2nd edition. Upper Saddle River: Prentice-Hall.

• DAS, B. (2007). Principles of Foundation Engineering. 6th edition. Toronto: Thomson.

Pile Capacity with Pile-Driving Formulas

Subscribe to our Mailing List!

Featured Posts

A Primer on NAND Flash Memories

Solidification Time and Chvorinov’s Rule

Step-Growth Polymerization, the Carothers Equation, and the Flory-Schulz Distribution

More Articles

Ballast Fouling in Railways

Drawdown in Aquifers: Theis and Hantush-Jacob Well Functions

Fields of Study

More

© 2024 Montogue Quiz

Subscribe to
our Mailing List!

Subscribe to our Mailing List!

Subscribe to receive our latest materials in your inbox.

Homework Help

© 2024 Montogue Quiz

Subscribe to our Mailing List!