1. The motivation for public-key cryptography
In the classical model of network security that dominated most applications until the mid-1970s, the two communicating parties, usually named “Alice” and “Bob,” must choose a secret key K. K then yields an encryption rule eK and a decryption rule dK. In a so-called secret-key or private-key cryptosystem, the exposure of either eK or dK renders the system insecure.
One crucial limitation of secret-key systems is that they require prior communication of the secret key K between Alice and Bob via a secure channel, before any ciphertext is transmitted. In many applications, this may be very difficult to achieve. For example, Bob and Alice, living in two distant places, may want to communicate using email. Finding a secure channel through which they can trade a secret key before communicating is bothersome, and perhaps impossible.
The idea behind a public-key cryptosystem is that one might conceive a cryptosystem where it is computationally infeasible to determine dK given eK. In the public-key cryptography framework, the encryption rule eK is a public key, which, as the name implies, can be made available to anyone, including some adversary “Eve.” Alice can send an encrypted message to Bob – without the nuisance of communicating a secret key beforehand – by using the public encryption rule eK. Bob will be the only person that can decrypt the ciphertext, using the decryption rule dK, which is called the private key. The entire public-key dynamic can be described by a simple analogy: Alice places an object in a metal box, and then locks it with a combination lock left there by Bob. Bob is the only person who can open the box since only he knows the combination.
Public-key cryptography was proposed by Whitfield Diffie and Martin Hellman in their famous 1976 paper, “New Directions in Cryptography.” A historical note: although public-key cryptography as a civilian technology was introduced by Diffie and Hellman, it appears that the technique entered military circles a few years earlier; specifically, James Ellis of the British Government Communications Headquarters (BGCH) introduced a technique equivalent to public-key encryption in 1969. However, Ellis’s work was kept classified until 1997.
A year after Diffie and Hellman published their concept paper, the first major public-key cryptosystem, now known as the RSA cryptosystem, was put forward. Its name draws from the trio of workers Ron Rivest, Adi Shamir, and Leonard Adleman (Fig. 1). (Returning to the issue of “military analysts preceding civilian workers,” it appears that a mathematician named Clifford Cocks, working in the same British agency mentioned above, wrote an internal document describing a version of the RSA algorithm in which the encryption exponent e was the same as the modulus N; this document was released in 1973, which would place Cocks four years ahead of the RSA team.)
Figure 1. Left to right: Ron Rivest, Adi Shamir, and Leonard Adleman.
2. The RSA algorithm
The steps of the RSA algorithm are listed in Figure 2.
Figure 2. Steps in the RSA cryptosystem.
Bob’s secret key is a pair of large primes p and q. His public key is the pair (N,e) consisting of the product N = pq and an encryption exponent e that is prime relatively to (p – 1)(q – 1). Alice takes her plaintext and converts it into an integer m between 1 and N. She encrypts m by computing the quantity
The integer c is her ciphertext, which she sends to Bob. It is then a simple matter for Bob to solve the congruence m 
In the encryption process, Alice calculates me (mod N). This can be done fairly quickly and without large memory using, for example, successive squaring. Here lies an advantage of employing modular arithmetic: If Alice tried to calculate me first, then reduce modulo-N, it is possible that recording me would overflow her computer’s memory. Similarly, the decryption process of calculating cd (mod N) can be done efficiently. Therefore, all the operations needed for encryption and decryption can be done reasonably quickly. The security is provided by the assumption that N cannot be factored.
One may wonder why Bob requires that gcd(e, (p – 1)(q – 1)) = 1. It can be shown that de
A crucial assumption in the implementation of RSA encryption is that Bob’s p and q are well chosen. Ideally, p and q should be selected at random, independently from each other. How large depends on the level of security needed. A simple recommendation is that the difference p – q should not be too small. If p – q is small, then p 
Example
Alice publishes her RSA public key: modulus N = 2038667 and exponent e = 103.
A) Bob wants to send Alice the message m = 892383. What ciphertext does Bob send to Alice?
B) Alice knows that her modulus factors into a product of two primes, one of which is p = 1301. Find a decryption exponent d for Alice.
C) Alice receives the ciphertext c = 317730 from Bob. Decrypt the message.
A) The ciphertext sent by Bob is
The operation above can be easily carried out with the Mathematica code
B) The modulus is N = 2038667 = 1301 
Again, Mathematica’s PowerMod command does the trick,
Thus, d = 810367 (mod 2035800).
C) Now, Alice needs to solve
Applying Mathematica’s PowerMod command a third time, we type
The decrypted message is 514407.
When it comes to security of the RSA cryptosystem, what does Eve, the adversary, do? The simplest mathematical attack to the RSA cryptosystem is to attempt to factor the modulus. Eve’s goal in this case is to compute the private key d which has the property that de
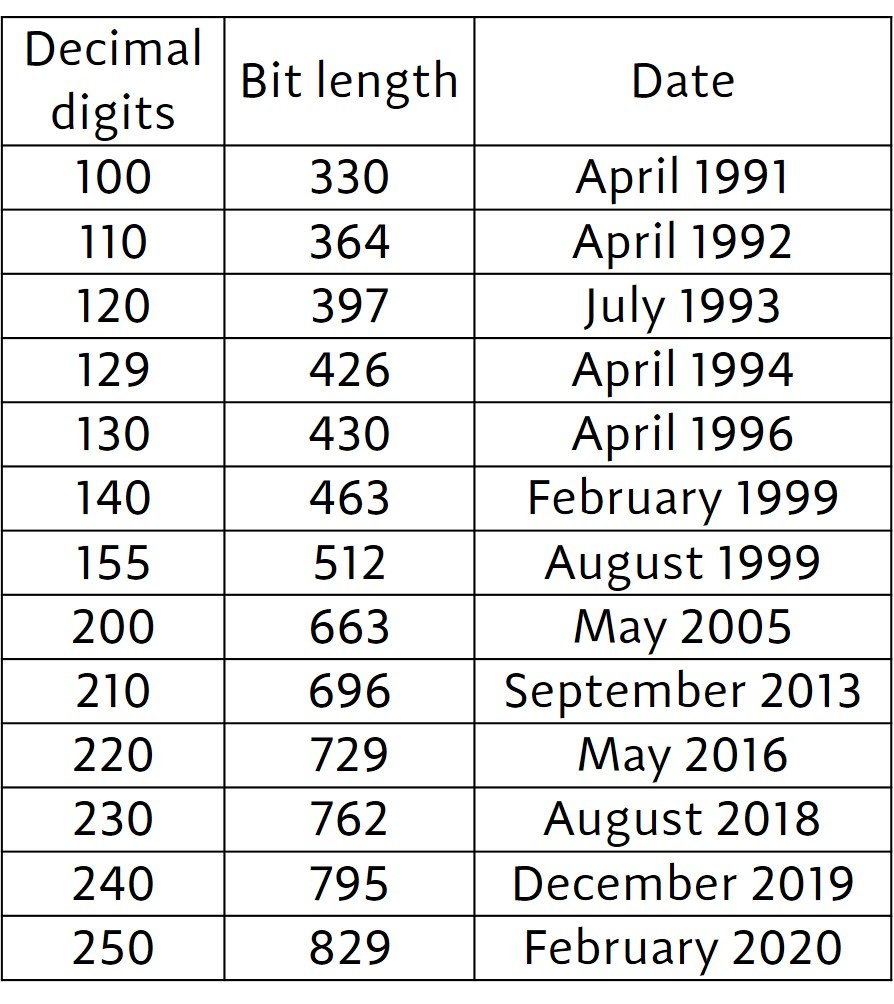
In order to prevent this attack, the modulus must be sufficiently large. This is the sole reason why moduli of 1024 or more bits are often recommended for a RSA scheme. The proposal of the RSA scheme in 1977 rekindled interest in the problem of integer factorization. One can even state that the major progress in integer factorization research in the past few decades wouldn’t have been possible were it not for interest in the RSA cryptosystem. Table 1 lists some of the RSA factoring records achieved since the 1990s. The first column lists the decimal digit count of the number that was factored; the second column lists the bit length of the number; the third column lists the month and year of the record. Wikipedia has details on the authorship of each record.
Table 1. RSA challenge factoring records.
3. Pollard’s p – 1 algorithm
The paradox of RSA is that in order to make RSA more efficient, we want to use a modulus N = pq that is as small as possible. On the other hand, if an opponent can factor N, then our encrypted messages are not secure. It is thus vital to understand how to factor large numbers, and in particular, to understand the capabilities of the different algorithms that are currently used for factorization. We close this article with a discussion on one such algorithm, a technique known as Pollard’s p – 1 method. Although not useful for all numbers, there are certain types of numbers for which it is quite efficient. Pollard’s method demonstrates that there are insecure RSA moduli that at first glance appear to be secure.
We begin with a number N = pq and a prespecified “bound” B, and our task is to determine the prime factors p and q. Assume that, using some arbitrary approach, we manage to find an integer L such that
This means that there are integers 
Consider what happens if we take a randomly chosen integer a and compute aL. From Fermat’s little theorem, we may write
(Here we have assumed that p does not divide a, and q does not divide a, which is likely because p and q are very large.) The exponent 
These relationships suggest that we can recover p through the simple gcd (greatest common divisor) computation
At this point one may ask, can we find an exponent L that is divisible by p – 1 but not by q – 1? Pollard noted that if p – 1 happens to be a product of many small primes, then it will divide factorial n! for some not-too-large value of integer n. Accordingly, for n = 2, 3, 4, …, we choose a value of a and compute
In practice, we might simply take a = 2. If the gcd is equal to 1, then we move on to the next value of n. If we get a number between 1 and N, a nontrivial factor of N has been found and we’re done. (There’s also the possibility that we get N itself; changing the value of a is one way to proceed in this case.)
To compute the number an! – 1 we must elevate a number to a power given by a factorial, which is known to be one of the fastest-growing operations in all math. Thus, the number in question is enormous, and computing it directly is unwieldy. However, we are interested only in the greatest common divisor of an! – 1 and N, so it suffices to determine
and then take the gcd with N. Thus we never need to work with numbers larger than N.
What’s more, there is no need to evaluate even the exponent n!. Instead, assuming that we have already computed an! mod N in the step above, we may compute the next value as
This leads to the algorithm described in Figure 3.
Figure 3. Steps in Pollard’s p – 1 factorization algorithm.
As an example, we can use Pollard’s p – 1 method to factor the number 220459. Using Mathematica, we find, with n = 3,
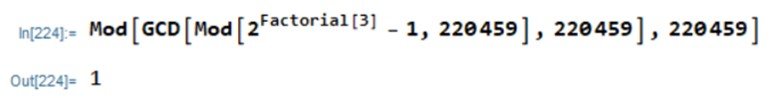
Proceeding similarly with n = 4,
The process can be automated, showing that the first nonunitary gcd is 449, which occurs when n = 8:
Dividing 220459 by 449 gives 491, so that 220459 = 449
Notice that it is easy for Bob and Alice to avoid the dangers of Pollard’s p – 1 method when creating RSA keys. They simply check that their secret primes have the property that neither p – 1 nor q – 1 factor entirely into small primes. Hoffstein et al. (2008) close their introduction to the algorithm at hand by noting that, from a cryptographic perspective, the importance of Pollard’s method lies in the following lesson. Most people would not expect, at first glance, that factorization properties of p – 1 and q – 1 have anything to do with the difficulty of factoring pq. The moral is that even if we build a cryptosystem based on a seemingly hard problem such as integer factorization, we must be wary of special cases of the problem that, for subtle and nonobvious reasons, are easier to solve than the general case.
References
• HOFFSTEIN, J., PIPHER, J. and SILVERMAN, J.H. (2008). An Introduction to Mathematical Cryptography. Berlin/Heidelberg: Springer.
• PAAR, C. and PELZL, J. (2010). Understanding Cryptography. Berlin/Heidelberg: Springer.
• STINSON, D.R. and PATERSON, M.B. (2019). Cryptography: Theory and Practice. 4th edition. Boca Raton: CRC Press.
• TRAPPE, W. and WASHINGTON, L.C. (2006). Introduction to Cryptography with Coding Theory. 2nd edition. Upper Saddle River: Pearson.
