Clairaut’s Theorem and Classical Physical Geodesy

In this article, I provide a quick introduction to some of the most important parameters and results of physical geodesy. Section 1 is a derivation of Clairaut’s theorem, an equation that bridges the geometric and gravitational facets of geodetic science. Section 2 introduces J₂, a coefficient, known by names such as “dynamic oblateness” (Stacey and Davis, 2008) and “dynamic form factor” (Buforn et al., 2012), that has grown in importance enormously since the advent of artificial satellites and thus deserves a few paragraphs of its own. The material of sections 1 and 2 is then applied in two example problems. The article closes with a section on Clairaut’s differential equation and how it can be related to the Earth’s shape, its internal density distribution, and beyond.

1. Flattening and Clairaut’s theorem

In the following developments, (u, $\displaystyle \beta$ , $\displaystyle \lambda$ ) denotes the elliptical coordinates of an arbitrary point.

Normal gravity, often denoted by $\displaystyle \gamma$ (gamma), is given by the negative gradient of the normal gravity potential U,

$\displaystyle \gamma =-\nabla U=-\frac{{\partial U}}{{\partial h}}=-\frac{1}{{{{s}_{u}}}}\frac{{\partial U}}{{\partial u}}\,\,\,(1)$

where

$\displaystyle {{s}_{u}}=\sqrt{{\frac{{{{u}^{2}}+{{E}^{2}}{{{\sin }}^{2}}\beta }}{{{{u}^{2}}+{{E}^{2}}}}}}$

is the line element for elliptical coordinate u, i.e. the change du that yields the distance change s_udu, h is the geodetic height, which is along the normal to the reference ellipsoid, and E is the linear eccentricity. Normal gravity on the ellipsoid ( $\displaystyle {{\gamma }_{0}}$ ) can be written in closed form as (Heiskanen and Moritz, 1967):

$\displaystyle {{\gamma }_{0}}=\frac{{GM}}{{{{a}^{2}}\Psi }}\left[ {1+m{e}'\frac{{{q}'\left( b \right)}}{{q\left( b \right)}}\left( {\frac{{{{{\sin }}^{2}}\beta }}{2}-\frac{1}{6}} \right)-m{{{\cos }}^{2}}\beta } \right]\,\,\,(2)$

Here, G is the gravitational constant, M is the mass of the Earth, a is the equatorial semiaxis, b is the polar semiaxis, $\displaystyle \Psi$ = (1 – e²cos² $\displaystyle \beta$ )^1/2, e’ = E/b, and

$\displaystyle m=\frac{{{{\omega }^{2}}{{a}^{2}}b}}{{GM}}\,\,\,(3)$

where $\displaystyle \omega$ is the angular velocity of the Earth. Also in equation 2,

$\displaystyle {q}'\left( u \right)=-\frac{{{{u}^{2}}+{{E}^{2}}}}{E}\frac{{dq}}{{du}}=3\left( {1+\frac{{{{u}^{2}}}}{{{{E}^{2}}}}} \right)\left[ {1-\frac{u}{E}\arctan \left( {\frac{E}{u}} \right)} \right]-1\,\,\,(4)$

where q is defined as

$\displaystyle iq\left( u \right)=\frac{i}{2}\left[ {\left( {1+\frac{{3{{u}^{2}}}}{{{{E}^{2}}}}} \right)\arctan \left( {\frac{E}{u}} \right)-3\frac{u}{E}} \right]\,\,\,(5)$

Using the formula above, normal gravities at the equator ( $\displaystyle \beta$ = 0) and poles ( $\displaystyle \beta$ = $\displaystyle \pm$ 90^o) are shown to be, respectively,

$\displaystyle {{\gamma }_{a}}=\frac{{GM}}{{ab}}\left[ {1-m-\frac{{m{e}'}}{6}\frac{{{q}'\left( b \right)}}{{q\left( b \right)}}} \right]\,\,\,(6)$

$\displaystyle {{\gamma }_{b}}=\frac{{GM}}{{{{a}^{2}}}}\left[ {1+\frac{{m{e}'}}{3}\frac{{{q}'\left( b \right)}}{{q\left( b \right)}}} \right]\,\,\,(7)$

Normal gravity at the equator, $\displaystyle {{\gamma }_{a}}$ , and normal gravity at the pole, $\displaystyle {{\gamma }_{b}}$ , satisfy the relation

$\displaystyle \frac{{a-b}}{a}+\frac{{{{\gamma }_{b}}-{{\gamma }_{a}}}}{{{{\gamma }_{a}}}}=\frac{{{{\omega }^{2}}b}}{{{{\gamma }_{a}}}}\left( {1+\frac{{{e}'{q}'\left( b \right)}}{{2q\left( b \right)}}} \right)\,\,\,(8)$

which I invite the reader to verify by substituting, in its left member, eqs. 6 and 7, along with b = a $\displaystyle \sqrt{{1-{{e}^{2}}}}$ and the definition of m.

In the 1920s, Somagliana (quoted in Sjöberg and Bagherbandi, 2017) developed an elegant closed formula for normal gravity on the ellipsoid,

$\displaystyle {{\gamma }_{0}}=\frac{{a{{\gamma }_{b}}{{{\sin }}^{2}}\beta +b{{\gamma }_{a}}{{{\cos }}^{2}}\beta }}{{\sqrt{{{{a}^{2}}{{{\sin }}^{2}}\beta +{{b}^{2}}{{{\cos }}^{2}}\beta }}}}=\frac{{a{{\gamma }_{a}}{{{\cos }}^{2}}\phi +b{{\gamma }_{b}}{{{\sin }}^{2}}\phi }}{{\sqrt{{{{a}^{2}}{{{\cos }}^{2}}\phi +{{b}^{2}}{{{\sin }}^{2}}\phi }}}}\,\,\,(9)$

where, in addition to familiar variables, we have the geocentric latitude $\displaystyle \phi$ . These equations show that, aside from the latitude terms $\displaystyle \beta$ or $\displaystyle \phi$ , normal gravity on the ellipsoid depends only on the four parameters a, b, $\displaystyle {{\gamma }_{a}}$ and $\displaystyle {{\gamma }_{b}}$ .

Hofmann-Wellenhof and Moritz (2005) develop an approximation to the gravity field that is linear relatively to the flattening f. The mathematical basis of the approximation is simple; first, note that the radius vector r of an ellipsoid can be approximated as

$\displaystyle r=a\left( {1-f{{{\sin }}^{2}}\phi } \right)\,\,\,(10)$

where a is equatorial radius, f is (terrestrial, geometric) flattening, and $\displaystyle \phi$ is the geocentric latitude. In a similar manner, the normal gravity $\displaystyle \gamma$ may be approximated as

$\displaystyle \gamma ={{\gamma }_{a}}\left( {1+f*{{{\sin }}^{2}}\phi } \right)\,\,\,(11)$

where $\displaystyle {{\gamma }_{a}}$ is normal gravity at the equator and f* is gravity flattening. For $\displaystyle \phi$ = 90^o, that is, at the poles, we have r = b and $\displaystyle \gamma$ = $\displaystyle {{\gamma }_{b}}$ , enabling us to solve eqs. 10 and 11 for f and f*, respectively, and obtain

$\displaystyle f=\frac{{a-b}}{a}$

$\displaystyle f*=\frac{{{{\gamma }_{b}}-{{\gamma }_{a}}}}{{{{\gamma }_{a}}}}$

Substituting f and f* into equation 8, we get

where

$\displaystyle m=\frac{{{{\omega }^{2}}a}}{{{{\gamma }_{a}}}}=\frac{{\text{Centrifugal force at equator}}}{{\text{Gravity at equator}}}\,\,\,(13)$

Equation 12 is Clairaut’s theorem in its original form. As pointed out by Hofmann-Wellenhof and Moritz (2005), this is one of the most striking formulas in physical geodesy, as it enables one to determine the geometrical flattening f from f* and m, which are purely dynamical quantities obtained by gravity measurements; that is, the flattening of the Earth can be determined from gravity measurements.

2. The dynamic oblateness or dynamic form factor J₂

The gravitational potential due to the Earth at points external to it satisfies Laplace’s equation. Solutions for this equation in spherical polar coordinates, that are appropriate for the Earth’s sphericity, can be found in Stacey and Davis (2008). In cases of axial symmetry, the potential variation on a spherical surface can be treated as a sum of Legendre polynomials, P_l(cos $\displaystyle \theta$ ), as given as functions of co-latitude $\displaystyle \theta$ for the first few integers l in Table 1. For each polynomial term the potential varies with radial distance from the center of the coordinate origin (the center of the Earth), $\displaystyle r$ , as $\displaystyle {{r}^{{-\left( {l+1} \right)}}}$ . Note that here we can ignore the $\displaystyle {{r}^{l}}$ alternative which applies to sources of potential external to the surface considered. Thus, with complete generality, we may write the gravitational potential V(r, $\displaystyle \theta$ ) (not to be confused with the normal potential U), due to an axially symmetrical body of mass M, as

$\displaystyle V=-\frac{{GM}}{r}\left( {{{J}_{0}}{{P}_{0}}-{{J}_{1}}\frac{a}{r}{{P}_{1}}\left( {\cos \theta } \right)-{{J}_{2}}{{{\left( {\frac{a}{r}} \right)}}^{2}}{{P}_{2}}\left( {\cos \theta } \right)-...} \right)\,\,\,(14)$

Here, a is the equatorial radius, G is the gravitational constant, and coefficients J₀, J₁, J₂, … represent the distribution of mass. By writing the equation in this form, we make these coefficients essentially dimensionless.

Since P₀ = 1, we must have J₀ = 1, because at great distances the first term becomes dominant and this gives the potential due to a point mass (or spherically symmetrical mass). By choosing the coordinate origin to be the center of mass, we must put J₁ = 0, because P₁ = cos $\displaystyle \theta$ and represents the off-center potential. Our particular interest is in the J₂ term, which is the principal one required to give the observed oblate ellipsoidal form of the geoid. All other terms are smaller by factors of order 1000 and can be reasonably neglected, including J₄, J₆, and so forth, even though they are required for the complete representation of an ellipsoid. Thus, with the explicit form of the function P₂, we can write the gravitational potential of the Earth as

$\displaystyle V=-\frac{{GM}}{r}+\frac{{GM{{a}^{2}}{{J}_{2}}}}{{{{r}^{3}}}}\left( {\frac{3}{2}{{{\cos }}^{2}}\theta -\frac{1}{2}} \right)\,\,\,(15)$

Stacey and Davis (2008) note that this is the potential at a stationary point, not rotating with the Earth, and that a rotating potential term must be added for points rotating with the Earth. Equation 15 gives the potential seen by satellites, including the Moon.

Table 1. Legendre polynomials $\displaystyle {{P}_{l}}$ (cos $\displaystyle \theta$ ) and associated polynomials, $\displaystyle {{p}_{{lm}}}$ (cos $\displaystyle \theta$ ). Numerical factors convert $\displaystyle {{P}_{{lm}}}$ to $\displaystyle p_{l}^{m}$

It is useful to express the dynamic form factor J₂ in terms of the principal moments of inertia of the Earth. To do so, we can appeal to MacCullagh’s formula, which gives the planet’s potential as

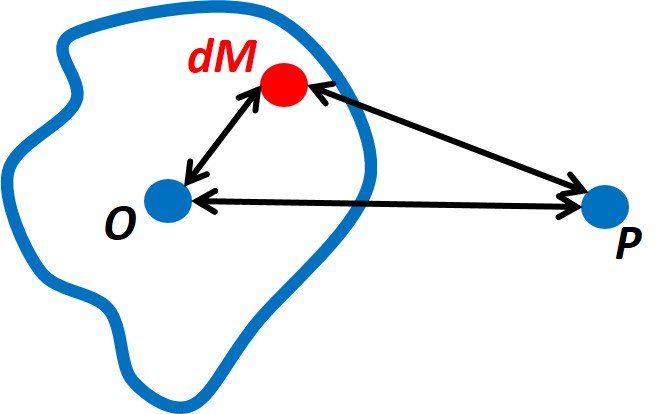
$\displaystyle V=-\frac{{GM}}{r}-\frac{G}{{2{{r}^{3}}}}\left( {A+B+C-3I} \right)-\left( {...} \right)\,\,\,(16)$

Here, A, B, and C are the moments of inertia of the Earth with respect to the x-, y-, and z-axes, respectively, and I is the moment of inertia of M about the axis OP (Figure 1). To identify equation 16 more closely with eq. 15, we write l in terms of A, B, C and the cosines l, m, n of the angles made by OP with the x, y, z axes:

$\displaystyle I=A{{l}^{2}}+B{{m}^{2}}+C{{n}^{2}}\,\,\,(17)$

where

$\displaystyle {{l}^{2}}+{{m}^{2}}+{{n}^{2}}=1\,\,\,(18)$

This is simplified by introducing rotational symmetry about z, so that B = A and, substituting for B in 17 and also for l² + m² by equation 18, we have

$\displaystyle I=A+\left( {C-A} \right){{n}^{2}}\,\,\,(19)$

and MacCullagh’s equation can be restated as

$\displaystyle V=-\frac{{GM}}{r}-\frac{G}{{2{{r}^{3}}}}\left( {C-A} \right)\left( {1-3{{n}^{2}}} \right)\,\,\,(20)$

Since n = cos $\displaystyle \theta$ , this is

$\displaystyle V=-\frac{{GM}}{r}+\frac{G}{{{{r}^{3}}}}\left( {C-A} \right)\left( {\frac{3}{2}{{{\cos }}^{2}}\theta -\frac{1}{2}} \right)\,\,\,(21)$

which coincides with equation 15 inasmuch as

$\displaystyle {{J}_{2}}=\frac{{\left( {C-A} \right)}}{{M{{a}^{2}}}}\,\,\,(22)$

From satellite orbits,

$\displaystyle {{J}_{2}}\approx 1.082626\times {{10}^{{-3}}}$

In the first-order approximation, J₂ can be related to flattening and the m coefficient by the simple expression

$\displaystyle f=\frac{3}{2}{{J}_{2}}+\frac{m}{2}\,\,\,(23)$

Figure 1. Points in the derivation of MacCullogh’s formula. dM is an infinitesimal mass element; O is the center of mass; P is an arbitrary point of interest. Moment of inertia I is determined with respect to axis OP. See Stacey and Davis (2008) for details.

Example 1

Point P is located at latitude 60^oS on the terrestrial ellipsoid and has a distance to its center equal to 6360.44 km. Earth’s mass is 5.9761 $\displaystyle \times$ 10²⁴ kg, the ratio between the polar and equatorial semiaxes is 0.9966, and the normal gravity at the equator is 978.032 Gal. Using the first-order approximation, determine the terrestrial flattening f, the dynamic oblateness J₂, and the normal gravity at P.

Noting that the polar-to-equatorial ratio equals 0.9966, determining the terrestrial flattening is straightforward,

$\displaystyle f=\frac{{a-b}}{a}=1-\frac{b}{a}$

$\displaystyle \therefore f=1-0.9966=3.4\times {{10}^{{-3}}}\leftarrow$

To find the dynamic oblateness J₂ from equation 23, we first need the m coefficient. This in turn calls for the equatorial radius a, which is given by

$\displaystyle r=a\left( {1-f{{{\sin }}^{2}}\phi } \right)\to a=\frac{r}{{1-f{{{\sin }}^{2}}\phi }}$

$\displaystyle \therefore a=\frac{{6360.44}}{{1-\left( {3.4\times {{{10}}^{{-3}}}} \right)\times {{{\sin }}^{2}}60{}^\text{o}}}=6376.70\,\,\text{km}$

so that, using the approximation a²b $\displaystyle \approx$ a³,

$\displaystyle m=\frac{{{{\omega }^{2}}{{a}^{3}}}}{{GM}}=\frac{{4{{\pi }^{2}}{{a}^{3}}}}{{{{T}^{2}}GM}}$

$\displaystyle \therefore m=\frac{{4{{\pi }^{2}}\times {{{\left( {6376.70\times {{{10}}^{3}}} \right)}}^{3}}}}{{{{{86,400}}^{2}}\times \left( {6.674\times {{{10}}^{{-11}}}} \right)\times \left( {5.9761\times {{{10}}^{{24}}}} \right)}}=3.438\times {{10}^{{-3}}}$

Substituting f and m into eq. 23 brings to

$\displaystyle f=\frac{3}{2}{{J}_{2}}+\frac{m}{2}\to {{J}_{2}}=\frac{{2f-m}}{3}$

$\displaystyle \therefore {{J}_{2}}=\frac{{2\times \left( {3.4\times {{{10}}^{{-3}}}} \right)-\left( {3.438\times {{{10}}^{{-3}}}} \right)}}{3}=1.121\times {{10}^{{-3}}}\leftarrow$

To find the normal gravity at point P, we first establish the gravity flattening via Clairaut’s theorem,

$\displaystyle f+f*=\frac{5}{2}m\to f*=\frac{5}{2}m-f$

$\displaystyle \therefore f*=\frac{5}{2}\times \left( {3.438\times {{{10}}^{{-3}}}} \right)-3.4\times {{10}^{{-3}}}=5.195\times {{10}^{{-3}}}$

so that

$\displaystyle {{\gamma }_{P}}={{\gamma }_{a}}\left( {1+f*{{{\sin }}^{2}}\phi } \right)=978.032\times \left[ {1+\left( {5.195\times {{{10}}^{{-3}}}} \right)\times {{{\sin }}^{2}}60{}^\text{o}} \right]$

$\displaystyle {{\gamma }_{P}}=981.843\,\,\text{Gal}\leftarrow$

Example 2 shows that Clairaut’s classical geodesy can also be applied with reasonable accuracy to other astronomical bodies, such as the Moon.

Example 2

Assuming that the Moon is an ellipsoid of equatorial radius 1738 km and polar radius 1737 km, with dynamic oblateness J₂ = 5.75374 $\displaystyle \times$ 10^-4 and a mass of 7.3483 $\displaystyle \times$ 10²² kg, calculate its period of rotation.

First, we calculate the (lunar) flattening f_M,

$\displaystyle {{f}_{M}}=\frac{{a-b}}{a}=\frac{{1738-1737}}{{1738}}=5.7537\times {{10}^{{-4}}}$

Then, we proceed to determine coefficient m,

$\displaystyle {{f}_{M}}=\frac{3}{2}{{J}_{2}}+\frac{m}{2}\to m=2{{f}_{M}}-3{{J}_{2}}$

$\displaystyle \therefore {{m}_{M}}=2\times \left( {5.75374\times {{{10}}^{{-4}}}} \right)-3\times \left( {3.81053\times {{{10}}^{{-4}}}} \right)=7.589\times {{10}^{{-6}}}$

From the definition of m, we can determine the period of rotation T,

$\displaystyle m=\frac{{{{\omega }^{2}}{{a}^{3}}}}{{GM}}\to T={{\left( {\frac{{4{{\pi }^{2}}{{a}^{3}}}}{{mGM}}} \right)}^{{{1}/{2}\;}}}$

$\displaystyle \therefore T={{\left[ {\frac{{4{{\pi }^{2}}\times {{{\left( {1738\times {{{10}}^{3}}} \right)}}^{3}}}}{{\left( {7.589\times {{{10}}^{{-6}}}} \right)\times \left( {6.674\times {{{10}}^{{-11}}}} \right)\times \left( {7.3483\times {{{10}}^{{22}}}} \right)}}} \right]}^{{{1}/{2}\;}}}=2.3598\times {{10}^{6}}\,\text{s}$

$\displaystyle \therefore T=27.312\,\,\text{days}\leftarrow$

3. Wahr’s (1996) rotating fluid sphere

Class notes by Wahr (1996) provide an interesting insight into the P₂ term that pops up over and over in classical geodetic models. Why does rotation causes such a term, he asks, and why are the results for J₂, f, and B₂ (the latter of which we do not address here) equal to the numbers that they are equal to? What do these numerical values tell us about the Earth?

It turns out, Wahr answers, that the numerical results are consistent with the assumption that the Earth responds to the centrifugal force of rotation as though it were a fluid. To understand this result, Wahr proposes a simple model of a spherically symmetric fluid sphere (density = constant on spherical surfaces). We spin the fluid about the z-axis with an angular velocity $\displaystyle \omega$ . After the fluid has come to equilibrium, what does the internal density distribution look like? Wahr’s model assumes the centrifugal force is much less than the gravitational force, so that surfaces of constant density are almost spheres – as they were before spin up. In other words, we assume that a surface of constant density which was r = r₀ before spin up, is now

$\displaystyle r={{r}_{0}}\left[ {1-\frac{2}{3}\sum\limits_{{l=0}}^{\infty }{{{{\varepsilon }_{l}}\left( {{{r}_{0}}} \right){{P}_{l}}\left( {\cos \theta } \right)}}} \right]\,\,\,(24)$

where $\displaystyle {{\varepsilon }_{l}}$ ( $\displaystyle {{r}_{0}}$ ) $\displaystyle \ll$ 1. The objective is to find the $\displaystyle {{\varepsilon }_{l}}$ ( $\displaystyle {{r}_{0}}$ ) for all $\displaystyle l$ and $\displaystyle {{r}_{0}}$ . One can derive integral/differential equations for all $\displaystyle {{\varepsilon }_{l}}$ , but Wahr circumscribes his work to $\displaystyle {{\varepsilon }_{2}}$ ; the reason is that, using the integral/differential equations for arbitrary l, it can be shown that $\displaystyle {{\varepsilon }_{l}}$ = 0 for $\displaystyle l$ $\displaystyle \ne$ 2. Physically, the reason is that the centrifugal potential includes only l = 2 aspherical terms.

Accordingly, Wahr models constant density/V_T (gravitational potential) surfaces with a shape described by

$\displaystyle r={{r}_{0}}\left[ {1-\frac{2}{3}\varepsilon \left( {{{r}_{0}}} \right){{P}_{2}}\left( {\cos \theta } \right)} \right]\,\,\,(25)$

where $\displaystyle \varepsilon$ $\displaystyle \ll$ 1. We need to find an equation for $\displaystyle \varepsilon$ (r₀). To do this, we need to find V_T at an arbitrary point (r, $\displaystyle \theta$ , $\displaystyle \phi$ ) inside the Earth. The centrifugal potential is straightforward,

$\displaystyle \frac{1}{3}{{\omega }^{2}}{{r}^{2}}-\frac{1}{3}{{\omega }^{2}}{{r}^{2}}{{P}_{2}}\left( {\cos \theta } \right)$

Finding the gravitational potential is much harder. Wahr presses on with a lengthy exercise on shell-shaped infinitesimal contributions to gravitational potential to find the overall gravitational potential V. To find V (r, $\displaystyle \theta$ , $\displaystyle \phi$ ) for the entire object, we sum over shells, that is, we integrate $\displaystyle {{V}_{{d{{r}_{0}}}}}$ over $\displaystyle {{r}_{0}}$ .

We must then determine $\displaystyle \varepsilon$ . With this purpose in mind, Wahr derives the following equation:

$\displaystyle -\frac{8}{5}\pi G\left\{ {\frac{1}{{r_{1}^{3}}}\int_{0}^{{{{r}_{1}}}}{{\rho \left( {{{r}_{0}}} \right)r_{0}^{4}}}\left[ {5\varepsilon \left( {{{r}_{0}}} \right)+{{r}_{0}}{{\partial }_{{r0}}}\varepsilon \left( {{{r}_{0}}} \right)} \right]d{{r}_{0}}+r_{1}^{2}\int_{{{{r}_{1}}}}^{a}{{\rho \left( {{{r}_{0}}} \right){{\partial }_{{r0}}}\varepsilon \left( {{{r}_{0}}} \right)d{{r}_{0}}}}-5\frac{{\varepsilon \left( {{{r}_{1}}} \right)}}{{{{r}_{1}}}}\int_{0}^{{{{r}_{1}}}}{{\rho \left( {{{r}_{0}}} \right)r_{0}^{2}d{{r}_{0}}}}} \right\}={{\omega }^{2}}r_{1}^{2}\,\,\,(26)$

using r₁ instead of r₀ to distinguish between the field (r₁) point and the mass (r₀) point. Equation 26 is an integral equation in $\displaystyle \varepsilon$ , but can be converted to a differential equation if we (1) multiply through by $\displaystyle r_{1}^{3}$ and take the derivative $\displaystyle {{\partial }_{{r1}}}$ of the result, then (2) multiply through by $\displaystyle r_{1}^{{-4}}$ and take $\displaystyle {{\partial }_{{r1}}}$ a second time. The result is Clairaut’s differential equation for $\displaystyle \varepsilon$ (r), which, after changing r₁ to r, has the form

$\displaystyle \frac{3}{{{{r}^{3}}}}\int_{0}^{r}{{\rho \left( {{{r}_{0}}} \right)r_{0}^{2}d{{r}_{0}}}}\left( {\frac{{{{\partial }^{2}}\varepsilon }}{{\partial {{r}^{2}}}}-\frac{6}{{{{r}^{2}}}}\varepsilon } \right)+\frac{{6\rho \left( r \right)}}{r}\left( {\frac{{\partial \varepsilon }}{{\partial r}}+\frac{\varepsilon }{r}} \right)=0\,\,\,(27)$

In condensed notation,

$\displaystyle \bar{\rho }\left( r \right)\left[ {\partial _{r}^{2}\varepsilon \left( r \right)-\frac{6}{{{{r}^{2}}}}\varepsilon \left( r \right)} \right]+\frac{{6\rho \left( r \right)}}{r}\left[ {{{\partial }_{r}}\varepsilon \left( r \right)+\frac{{\varepsilon \left( r \right)}}{r}} \right]=0\,\,\,(28)$

where

$\displaystyle \bar{\rho }\left( r \right)=\frac{3}{{{{r}^{3}}}}\int_{0}^{r}{{\rho \left( {{{r}_{0}}} \right)r_{0}^{2}d{{r}_{0}}}}$

As an example, Wahr assumes $\displaystyle \rho$ = $\displaystyle {{\rho }_{0}}$ = constant. Then,

$\displaystyle \bar{\rho }\left( r \right)=\frac{3}{{{{r}^{3}}}}{{\rho }_{0}}\int_{0}^{r}{{r_{0}^{2}d{{r}_{0}}}}={{\rho }_{0}}\,\,\,(29)$

In this case, Clairaut’s equation reduces to

$\displaystyle \frac{{{{\partial }^{2}}\varepsilon }}{{\partial {{r}^{2}}}}+\frac{6}{r}\frac{{\partial \varepsilon }}{{\partial r}}=0\,\,\,(30)$

Wahr proposes a solution of the form $\displaystyle \varepsilon$ = $\displaystyle {{r}^{n}}$ , which, when substituted above, yields

$\displaystyle n\left( {n-1} \right)+6n=0$

$\displaystyle \therefore n\left( {n+5} \right)=0$

so n = 0 or n = –5. It follows that the general solution has the form

$\displaystyle \varepsilon =\alpha +\frac{\beta }{{{{r}^{5}}}}\,\,\,(31)$

It remains to determine coefficients $\displaystyle \alpha$ and $\displaystyle \beta$ . We note right away that $\displaystyle \beta$ = 0, otherwise $\displaystyle \varepsilon \to \infty$ near the Earth’s center; this would imply that radii of constant density/potential surfaces $\displaystyle \to \infty$ near the center, which we know cannot be true. So $\displaystyle \beta$ = 0 and the general solution is $\displaystyle \varepsilon$ = $\displaystyle \alpha$ = constant. To find $\displaystyle \alpha$ in terms of $\displaystyle {{\omega }^{2}}$ , we put $\displaystyle \varepsilon$ = $\displaystyle \alpha$ into integral equation 26 so that, with $\displaystyle {{\partial }_{{r0}}}\varepsilon =0$ , the equation reduces to

$\displaystyle -\frac{8}{{15}}\pi G\left( {\frac{1}{{r_{1}^{3}}}5\alpha {{\rho }_{0}}\int_{0}^{{{{r}_{1}}}}{{r_{0}^{4}d{{r}_{0}}}}-5\frac{\alpha }{{{{r}_{1}}}}{{\rho }_{0}}\int_{0}^{{{{r}_{1}}}}{{r_{0}^{2}d{{r}_{0}}}}} \right)=\frac{1}{3}{{\omega }^{2}}r_{1}^{2}$

$\displaystyle \therefore -\frac{8}{{15}}\pi G\left( {\frac{{5\alpha {{\rho }_{0}}}}{{r_{1}^{3}}}\frac{{r_{1}^{5}}}{5}-5\frac{\alpha }{{{{r}_{1}}}}{{\rho }_{0}}\frac{{r_{1}^{3}}}{3}} \right)=\frac{1}{3}{{\omega }^{2}}r_{1}^{2}$

$\displaystyle \therefore \alpha =\frac{{15{{\omega }^{2}}}}{{16\pi {{\rho }_{0}}G}}\,\,\,(32)$

The real density inside the Earth is not constant, but increases with depth. It turns out that Clairaut’s equation implies that $\displaystyle \varepsilon$ increases with radius. So the outer portions of Wahr’s fluid Earth are more aspherical than the inner portions.

$\displaystyle \varepsilon$ also turns out to be positive, which implies that the surfaces are squashed down at the poles. To see this, note that (remembering that $\displaystyle {{P}_{2}}$ = (1/2)(3cos $\displaystyle \theta$ – 1)):

$\displaystyle r\left( {\theta =90{}^\text{o}} \right)-r\left( {\theta =0{}^\text{o}} \right)=-\frac{2}{3}\varepsilon {{r}_{0}}\left[ {{{P}_{2}}\left( {90{}^\text{o}} \right)-{{P}_{2}}\left( {0{}^\text{o}} \right)} \right]$

$\displaystyle \therefore r\left( {\theta =90{}^\text{o}} \right)-r\left( {\theta =0{}^\text{o}} \right)=-\frac{2}{3}\varepsilon {{r}_{0}}\left( {-\frac{1}{2}-1} \right)=\varepsilon {{r}_{0}}$

So, $\displaystyle \varepsilon$ > 0 and r(90º) > r(0º).

Finally, Wahr (1996) notes that, using the best seismic results for the density function $\displaystyle \rho$ ( $\displaystyle {{r}_{0}}$ ) and solving Clairaut’s equation, a flattening of 1/299.7 is obtained. The observed f, using satellite data, is about 1/298.257, indicating good agreement; but observational errors for J₂, another parameter of interest, are better than 10^-6. Why is there a substantial error in the estimate for flattening? Wahr presses on to discuss this phenomenon, adding yet another parameter, the dynamical ellIpticity, to the mix. It turns out that the Clairaut equation is not a good predictor of this latter quantity, either.

One possible reason for the poor prediction of flattening/dynamical ellipticity in the Clairaut model is that the mantle is a very viscous fluid and, in view of its exceptionally large viscosity, it takes a reasonably long time for the mantle to reach equilibrium. The relevance of this is that the Earth’s rotation is decreasing approximately linearly with time, and so the centrifugal force is decreasing. If the viscosity is high enough that the mantle response time is longer than the time it takes for the centrifugal force to decrease significantly, then the present shape of the Earth might be reflecting the older, faster rotation. This would lead to ellipticities larger than those predicted from Clairaut’s equation. Most geophysicists do not subscribe to this explanation, however. Indeed, estimates of mantle viscosity from postglacial rebound suggest the viscosity is not large enough to support this hypothesis.

Wahr concludes that the most likely explanation is that the Earth is approximately fluid over long time periods, but that there are other factors besides rotation that cause lateral variations in density. That is certainly the case: thermal anomalies must exist within the Earth if there is to be ongoing mantle convection. Those thermal anomalies must be associated with density anomalies (it is buoyancy forces caused by the density anomalies that directly drive the convection). So, presumably the discrepancy from Clairaut’s equation is due to the spherico-harmonic $\displaystyle Y_{2}^{0}$ component of those thermal/density anomalies.

References

• BUFORN, E., PRO, C. and UDÍAS, A. (2012). Solved Problems in Geophysics. Cambridge: Cambridge University Press.

• HEISKANEN, W. and MORITZ, H. (1967). Physical Geodesy. New York: W.H. Freeman.

• HOFMANN-WELLENHOF, B. and MORITZ, H. (2005). Physical Geodesy. Vienna: Springer Wien.

• SJÖBERG, L. and BAGHERBANDI, B. (2017). Gravity Inversion and Gravitation. Berlin/Heidelberg: Springer.

• STACEY, M. and DAVIS, F. (2008). Physics of the Earth. 4th edition. Cambridge: Cambridge University Press.

• WAHR, J. (1996). Geodesy and Gravity: Class Notes. Boulder: University of Colorado.

Clairaut’s Theorem and Classical Physical Geodesy

Subscribe to our Mailing List!

Featured Posts

A Primer on NAND Flash Memories

Solidification Time and Chvorinov’s Rule

Step-Growth Polymerization, the Carothers Equation, and the Flory-Schulz Distribution

More Articles

Air Pollution and the Gaussian Plume Model

River Meandering Models

Fields of Study

More

© 2024 Montogue Quiz

Subscribe to
our Mailing List!

Subscribe to our Mailing List!

Subscribe to receive our latest materials in your inbox.

Homework Help

© 2024 Montogue Quiz

Subscribe to our Mailing List!