Heat Flow and Rifting in the Lithosphere: Oceanic and Continental

In this article, I apply basic math to derive some interesting results on the geodynamics of oceanic and continental lithosphere. In section 1, I use the half-space model to derive relations for the geothermal flow and depth of the seafloor. In section 2, I introduce McKenzie’s model of subsidence and include a simple spreadsheet that readers are free to play around with. Finally, section 3 is dedicated to continental lithosphere and the concept of heat flow province, which I illustrate with a solved example.

1. Heat flow and oceanic depth

Thermal conditions of an oceanic plate are different from those of a continental plate, because the material cools as it moves away from the ridge and the radiogenic heat in the crust is negligible. The simplest thermal model of oceanic lithosphere is to consider a semi-infinite half-space. If x and z are the horizontal and vertical coordinates, respectively, and v = dx/dt denotes the plate velocity, assumed to be constant and in practice determined by the age t of the crust at a distance x from the ridge, we may write

$\displaystyle \frac{{\partial T}}{{\partial t}}=\frac{{\partial T}}{{\partial x}}\frac{{dx}}{{dt}}=v\frac{{\partial T}}{{\partial x}}\,\,\,(1)$

Further, if horizontal heat conduction is negligible compared to heat conduction by the plate’s vertical motion, the Laplacian of temperature can be simplified as

$\displaystyle {{\nabla }^{2}}T=\frac{{{{\partial }^{2}}T}}{{\partial {{x}^{2}}}}+\frac{{{{\partial }^{2}}T}}{{\partial {{z}^{2}}}}\approx \frac{{{{\partial }^{2}}T}}{{\partial {{z}^{2}}}}\,\,\,(2)$

It follows that the Fourier equation simplifies to

$\displaystyle {{\nabla }^{2}}T=\frac{1}{\kappa }\frac{{\partial T}}{{\partial t}}\to \frac{{{{\partial }^{2}}T}}{{\partial {{z}^{2}}}}=\frac{v}{\kappa }\frac{{\partial T}}{{\partial x}}\,\,\,(3)$

where $\displaystyle \kappa$ is thermal diffusivity. The problem of finding T(x,z) in a moving plate is then equivalent to finding T(z,t) in a stationary plate. If one considers that plate cooling is similar to a semi-infinite solid initially at temperature T_s and with surface maintained at temperature T₀, the solution to (3) can be shown to be

$\displaystyle \frac{{T\left( {z,t} \right)-{{T}_{0}}}}{{{{T}_{s}}-{{T}_{0}}}}=\text{erf}\left( {\frac{z}{{2\sqrt{{\kappa t}}}}} \right)\,\,\,(4)$

where erf denotes the Gaussian error function. Equation (4) provides the temperature distribution along the plate with age. One immediate application of this result is the calculation of the geothermal flow q₀. Rearranging (4) gives

$\displaystyle T={{T}_{0}}+\left( {{{T}_{s}}-{{T}_{0}}} \right)\frac{2}{{\sqrt{\pi }}}\int_{0}^{{{z}/{{\sqrt{{4\kappa t}}}}\;}}{{{{e}^{{-{{u}^{2}}}}}d{u}'}}\,\,\,(5)$

where u = z/(4 $\displaystyle \kappa$ t)^1/2. Differentiating and applying the Leibniz rule, we find the thermal gradient

$\displaystyle \frac{{dT}}{{dz}}=\frac{{{{T}_{s}}-{{T}_{0}}}}{{\sqrt{{\pi \kappa t}}}}\exp \left( {-\frac{{{{z}^{2}}}}{{4\kappa t}}} \right)\,\,\,(6)$

Noting that geothermal flow equals the product of thermal conductivity and geothermal gradient, it follows that, with z = 0,

$\displaystyle {{q}_{0}}=k\frac{{\left( {{{T}_{s}}-{{T}_{0}}} \right)}}{{\sqrt{{\pi \kappa t}}}}=k\left( {{{T}_{s}}-{{T}_{0}}} \right){{\left( {\frac{v}{{\pi \kappa x}}} \right)}^{{{1}/{2}\;}}}\,\,\,(7)$

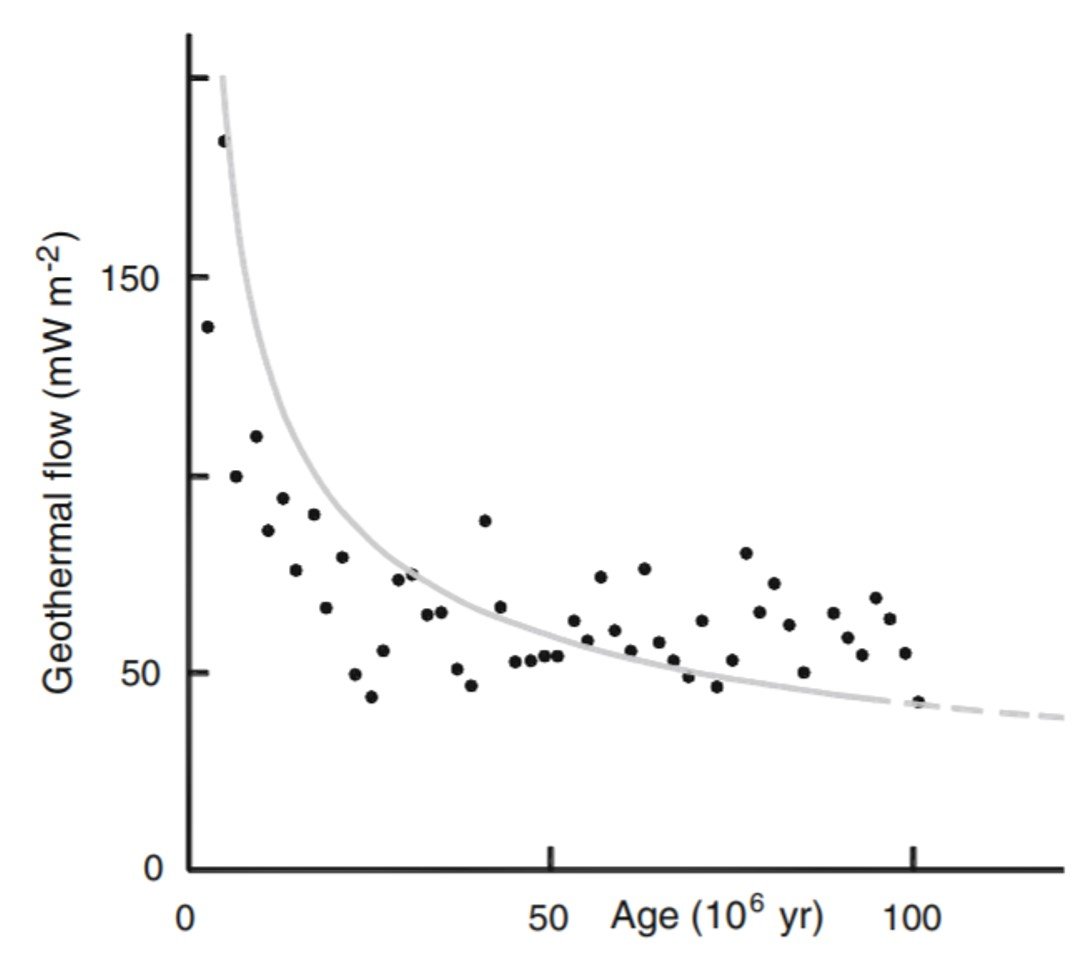
This result shows that, except for factor $\displaystyle {{\pi }^{{-{1}/{2}\;}}}$ , the heat flux into the rock is k times the temperature difference (T_s – T₀) divided by the thermal diffusion length $\displaystyle \sqrt{{\kappa t}}$ . Equation (7) indicates that geothermal flow q₀ decreases with age (or distance from ridge axis), a trend that has been confirmed by experimental data (Figure 1). However, the correlation is somewhat poor in the case of younger material (t $\displaystyle \le$ 40 Myr), for which the observed q₀ is less than expected. This is due to convective cooling caused by hydrothermal circulation in the crust next to the oceanic ridges. As age increases, the sedimentary cover (less permeable than fractured basalts) prevents the seawater infiltration into the oceanic crust and consequently hinders convective cooling. For t $\displaystyle \ge$ 80 Myr, the observed q₀ reaches an asymptotic value, given by the heat flow from the asthenosphere plus the heat flow produced by the radioactive elements of the oceanic plate.

Figure 1. Geothermal heat flow perpendicular to ridge as a function of age. The solid curve is equation (7) and the data points are taken from Stein and Stein (1992).

Note that an undesirable feature of equation (7) is that it yields an infinite heat flux at t = 0. A simple workaround would be to use the total heat H instead; H is given by integrating q₀ from t = 0 to t,

$\displaystyle H=\int_{0}^{t}{{{{q}_{0}}dt}}=\frac{{2k\left( {{{T}_{0}}-{{T}_{1}}} \right)}}{{\sqrt{{\pi \kappa }}}}\sqrt{t}\,\,\,(8)$

In the mid-1800s, William Thompson, later Lord Kelvin, used the theory for the conductive cooling of a semi-infinite half-space to estimate the age of the Earth. He hypothesized that the Earth was formed at a uniform temperature T₁ and that its surface was subsequently maintained at a low temperature T₀. He assumed that a thin near-surface boundary layer developed as the Earth cooled. Since the boundary layer would be thin compared with the radius of the Earth, he reasoned that the one-dimensional model developed in this section could be applied. Using an equation similar to (7), he concluded that the age of the Earth t₀ was given by

$\displaystyle {{q}_{0}}=k{{\left( {\frac{{dT}}{{dz}}} \right)}_{0}}=k\frac{{\left( {{{T}_{1}}-{{T}_{0}}} \right)}}{{\sqrt{{\pi \kappa {{t}_{0}}}}}}$

$\displaystyle \therefore {{t}_{0}}=\frac{{{{{\left( {{{T}_{1}}-{{T}_{0}}} \right)}}^{2}}}}{{\pi \kappa \left( {{{dT}}/{{dz}}\;} \right)_{0}^{2}}}\,\,\,(9)$

where dT/dz is the present near-surface thermal gradient. With dT/dz = 25 K/km, T₁ – T₀ = 2000 K, and $\displaystyle \kappa$ = 1 mm²/s, the age of the Earth from equation (9) can be calculated to be

$\displaystyle {{t}_{0}}=\frac{{{{{2000}}^{2}}}}{{\pi \times {{{10}}^{{-6}}}\times {{{\left( {25\times {{{10}}^{{-3}}}} \right)}}^{2}}}}=2.04\times {{10}^{{15}}}\,\text{s}$

or approximately 65 million years. One of the reasons why this approximation misses the real value of 4.54 billion years by such a large margin is that it does not account for radiogenic heat. It was not until radioactivity was discovered at about 1900 that Kelvin’s estimate was seriously questioned.

Since the oceanic lithosphere is approximately in isostatic equilibrium, the average seafloor depth should increase with age as a consequence of the density increase caused by cooling. The principle of isostasy states that there is the same mass per unit area between the surface and the depth of compensation for any vertical column of material. Thus, by denoting with h_w the depth of the ocean floor, h_l and $\displaystyle \rho$ the thickness and density of the lithosphere, $\displaystyle {{\rho }_{w}}$ and $\displaystyle {{\rho }_{m}}$ the densities of water and astenospheric mantle, we may write

$\displaystyle {{\rho }_{m}}\left( {{{h}_{w}}+{{h}_{l}}} \right)={{\rho }_{w}}{{h}_{w}}+\int_{0}^{{{{h}_{l}}}}{{\rho dz}}\,\,\,(10)$

$\displaystyle {{h}_{w}}\left( {{{\rho }_{m}}-{{\rho }_{w}}} \right)=\int_{0}^{{{{h}_{l}}}}{{\left( {\rho -{{\rho }_{m}}} \right)dz}}\,\,\,(11)$

where $\displaystyle \rho$ > $\displaystyle {{\rho }_{m}}$ because of the thermal contraction of the cooling lithosphere. Densities and temperatures are linearly related through the volume expansion coefficient $\displaystyle \alpha$ ,

$\displaystyle \rho -{{\rho }_{m}}=\alpha {{\rho }_{m}}\left( {{{T}_{s}}-T} \right)\,\,\,(12)$

so that, substituting in (11), we have

$\displaystyle {{h}_{w}}\left( {{{\rho }_{m}}-{{\rho }_{w}}} \right)=\alpha {{\rho }_{m}}\int_{0}^{{{{h}_{l}}}}{{\left( {{{T}_{s}}-T} \right)dz}}\,\,\,(13)$

Substituting the temperature profile from (7), we write

$\displaystyle {{h}_{w}}\left( {{{\rho }_{m}}-{{\rho }_{w}}} \right)=\alpha {{\rho }_{m}}\left( {{{T}_{s}}-{{T}_{0}}} \right)\int_{0}^{\infty }{{\left[ {\text{erfc}\left( {\frac{z}{{2\sqrt{{\kappa t}}}}} \right)} \right]dz}}\,\,\,(14)$

where we have changed the upper bound of the integral from z = h_l to z = $\displaystyle \infty$ because $\displaystyle \rho$ $\displaystyle \to$ $\displaystyle {{\rho }_{m}}$ and T $\displaystyle \to$ T_s at the base of the lithosphere. At this point, we introduce the variable u = z/(4 $\displaystyle \kappa$ t)^1/2, so that

$\displaystyle {{h}_{w}}\left( {{{\rho }_{m}}-{{\rho }_{w}}} \right)=\alpha {{\rho }_{m}}\left( {{{T}_{s}}-{{T}_{0}}} \right){{\left( {\kappa t} \right)}^{{{1}/{2}\;}}}\int_{0}^{\infty }{{\text{erfc}\left( u \right)d{u}'}}\,\,\,(15)$

Here, we appeal to the standard result

$\displaystyle \int_{0}^{\infty }{{\text{erfc}\left( u \right)d{u}'=\frac{1}{{\sqrt{\pi }}}}}\,\,\,(16)$

so that

$\displaystyle {{h}_{w}}=\frac{{2\alpha {{\rho }_{m}}\left( {{{T}_{s}}-{{T}_{0}}} \right)}}{{{{\rho }_{m}}-{{\rho }_{w}}}}{{\left( {\frac{{\kappa t}}{\pi }} \right)}^{{{1}/{2}\;}}}\,\,\,(17)$

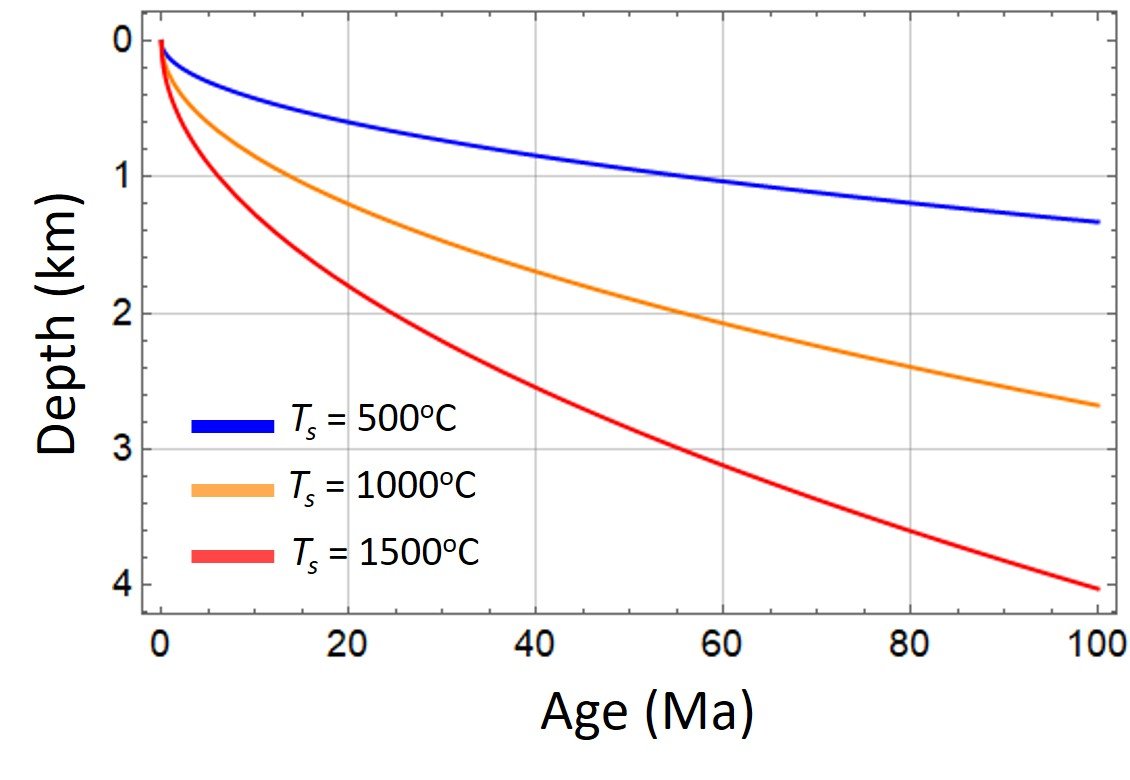
This expression shows that, if isostatic conditions prevail, the average depth of the ocean will increase with the square root of age. Figure 2 plots equation (17) for three temperatures T_s = 500^oC, 1000^oC, and 1500^oC.

Figure 2. Evolution of oceanic depth given by equation (17) for for three temperatures T_s. Values used were $\displaystyle \alpha$ = 3 $\displaystyle \times$ 10^-5 ^oC^-1, $\displaystyle {{\rho }_{m}}$ = 3300 kg/m³, $\displaystyle {{\rho }_{w}}$ = 1030 kg/m³, T₀ = 5^oC, and $\displaystyle \kappa$ = 30 km²/Ma.

2. McKenzie’s (1978) subsidence model

McKenzie (1978) used the observations of the deep structure of rift-type basins together with the exponential nature of their subsidence to suggest a kinematic model for rift-type basin evolution, which predicts subsidence and uplift, crustal thinning, and heat flow for different times since rifting. He showed that, as a consequence of extension, there is an initial subsidence due to crustal thinning followed by a thermal subsidence as the stretched lithosphere cools. Consider some initial thickness of the crust, t_c, and lithosphere, a, a steady-state geothermal gradient in the lithosphere (which includes the crust) and an isothermal sub-lithospheric mantle. If the temperature at the surface of the lithosphere is 0^oC and the temperature at its base is T₁, then the average temperature at the base of the crust is given by

$\displaystyle \frac{{{{T}_{1}}{{t}_{c}}}}{{2a}}\,\,\,(18)$

Similarly, the average temperature in the sub-crustal mantle is

$\displaystyle \frac{{\left( {{{{{T}_{1}}{{t}_{c}}}}/{a}\;} \right)+{{T}_{1}}}}{2}=\frac{{{{T}_{1}}\left( {{{t}_{c}}+a} \right)}}{{2a}}\,\,\,(19)$

The pressure at the base of the unstretched column is given by

$\displaystyle {{\rho }_{c}}g{{t}_{c}}+{{\rho }_{l}}g\left( {a-{{t}_{c}}} \right)\,\,\,(20)$

where

$\displaystyle {{\rho }_{c}}={{\rho }_{{c0}}}\left( {1-\frac{{\alpha {{T}_{1}}{{t}_{c}}}}{{2a}}} \right)\,\,\,(21)$

$\displaystyle {{\rho }_{l}}={{\rho }_{{l0}}}\left[ {1-\frac{{\alpha {{T}_{1}}\left( {{{t}_{c}}+a} \right)}}{{2a}}} \right]\,\,\,(22)$

and $\displaystyle \alpha$ is the coefficient of volume expansion, $\displaystyle {{\rho }_{{l0}}}$ is the density of the lithosphere at 0^oC and $\displaystyle {{\rho }_{{c0}}}$ is the density of the crust at 0^oC. Substituting (21) and (22) into (20) gives for pressure,

$\displaystyle {{\rho }_{{c0}}}\left( {1-\frac{{\alpha {{T}_{1}}{{t}_{c}}}}{{2a}}} \right)g{{T}_{c}}+{{\rho }_{{l0}}}\left[ {1-\frac{{\alpha {{T}_{1}}\left( {{{t}_{c}}+a} \right)}}{{2a}}} \right]g\left( {a-{{t}_{c}}} \right)\,\,\,(23)$

The effect of rifting is to thin the crust and lithosphere and to raise the geotherm. We can write the thickness of the thinned crust as t_c/ $\displaystyle {{\beta }_{s}}$ and the thickness of the crustal mantle as a/ $\displaystyle {{\beta }_{s}}$ – t_c/ $\displaystyle {{\beta }_{s}}$ , where $\displaystyle {{\beta }_{s}}$ is the stretching factor. The pressure at the base of the stretched column then becomes

$\displaystyle {{\rho }_{w}}{{S}_{i}}g+{{\rho }_{{c0}}}\left( {1-\frac{{\alpha {{T}_{1}}{{t}_{c}}}}{{2a}}} \right)g\frac{{{{t}_{c}}}}{{{{\beta }_{s}}}}+{{\rho }_{{l0}}}\left[ {1-\frac{{\alpha {{T}_{1}}\left( {{{t}_{c}}+a} \right)}}{{2a}}} \right]g\left( {\frac{a}{{{{\beta }_{s}}}}-\frac{{{{t}_{c}}}}{{{{\beta }_{s}}}}} \right)+{{\rho }_{{l0}}}\left( {1-\alpha {{T}_{1}}} \right)g\left( {a-{{S}_{i}}-\frac{a}{{{{\beta }_{s}}}}} \right)\,\,\,(24)$

where S_i is initial subsidence and $\displaystyle {{\rho }_{w}}$ is the density of water. Combining equations (23) and (24) brings to

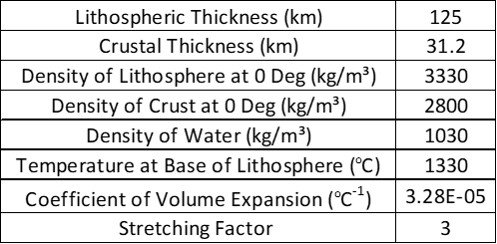
$\displaystyle {{S}_{i}}=\frac{{a\left[ {\left( {{{\rho }_{{l0}}}-{{\rho }_{{co}}}} \right)\frac{{{{t}_{c}}}}{a}\left( {1-\frac{{\alpha {{T}_{1}}{{t}_{c}}}}{{2a}}} \right)-\frac{{{{\rho }_{{l0}}}\alpha {{T}_{1}}}}{2}} \right]\left( {1-\frac{1}{{{{\beta }_{s}}}}} \right)}}{{{{\rho }_{{l0}}}\left( {1-\alpha {{T}_{1}}} \right)-{{\rho }_{w}}}}\,\,\,(25)$

This equation gives the initial subsidence for different values of initial thickness, temperature, density of crust and sub-crustal mantle, and stretching factor. This is a lengthy formula, so I’ve set up a simple spreadsheet to automate calculations; download it here. Using the sample values listed in Table 1, the spreadsheet returns densities $\displaystyle {{\rho }_{c}}$ = 2785 kg/m³, $\displaystyle {{\rho }_{l}}$ = 3239 kg/m³, and initial subsidence S_i = 2.279 km. Note that, as the crust is stretched, the densities of the crust and mantle decrease and the lithosphere subsides (S_i > 0).

Table 1. Data for sample subsidence calculations

The final subsidence can be obtained by balancing the pressure at the base of the unstretched column with the final column. The pressure at the base of the unstretched column is given by (23). The pressure at the base of the final column is, in turn,

$\displaystyle {{\rho }_{w}}g{{S}_{f}}+{{{\rho }'}_{c}}\frac{{{{t}_{c}}}}{{{{\beta }_{s}}}}g+{{{\rho }'}_{l}}\left( {a-{{S}_{f}}-\frac{{{{t}_{c}}}}{{{{\beta }_{s}}}}} \right)g\,\,\,(26)$

where $\displaystyle {{{\rho }'}_{c}}$ is the density of the cooled stretched crust and $\displaystyle {{{\rho }'}_{l}}$ is the density of the cooled sub-crustal mantle. Equating (23) and (26) and rearranging gives

$\displaystyle {{S}_{f}}=\frac{{a\left( {{{{{\rho }'}}_{l}}-{{\rho }_{l}}} \right)+{{t}_{c}}\left( {{{\rho }_{l}}+\frac{{{{{{\rho }'}}_{c}}}}{{{{\beta }_{s}}}}-\frac{{{{{{\rho }'}}_{l}}}}{{{{\beta }_{s}}}}-{{\rho }_{c}}} \right)}}{{{{{{\rho }'}}_{l}}-{{\rho }_{w}}}}\,\,\,(27)$

where $\displaystyle {{\rho }_{c}}$ is the density of crust before stretching and $\displaystyle {{\rho }_{l}}$ is the density of the sub-crustal mantle before stretching; these have been defined above. The values of $\displaystyle {{{\rho }'}_{c}}$ and $\displaystyle {{{\rho }'}_{l}}$ can be expressed in terms of the coefficient of volume expansion and the new, cooled temperature structure; that is,

$\displaystyle {{{\rho }'}_{c}}={{\rho }_{{c0}}}\left( {1-\frac{{\alpha {{T}_{1}}{{t}_{c}}}}{{2{{\beta }_{s}}a}}} \right)\,\,\,(28)$

$\displaystyle {{{\rho }'}_{l}}={{\rho }_{{l0}}}\left( {1-\frac{{\alpha {{T}_{1}}{{t}_{c}}}}{{2a{{\beta }_{s}}}}-\frac{{\alpha {{T}_{1}}}}{2}} \right)\,\,\,(29)$

Using the same parameters as before, we obtain $\displaystyle {{{\rho }'}_{c}}$ = 2795 kg/m³, $\displaystyle {{{\rho }'}_{l}}$ = 3251 kg/m³ and S_f = 4.927 km. Therefore, the densities of the crust and lithosphere increase from initial conditions and the lithosphere subsides.

The thermal subsidence, $\displaystyle \sigma$ , is given by the difference between final and initial subsidence:

$\displaystyle \sigma ={{S}_{f}}-{{S}_{i}}\,\,\,(30)$

Substituting the values for S_i and S_f above gives $\displaystyle \sigma$ = 2.648 km. The initial and thermal subsidence are therefore similar. Watts (2001) notes that we have so far computed the subsidence at two “end member” points: one corresponding to the onset of rifting and the other after a long time has elapsed since rifting. The intermediate values of subsidence can be established by using the Fourier equation, which relates the temperature, T, at a time since rifting, t, to z, the depth measured downwards, and $\displaystyle \kappa$ , the thermal diffusivity of the lithosphere:

$\displaystyle \frac{{\partial T}}{{\partial t}}=\kappa \frac{{{{\partial }^{2}}T}}{{\partial {{z}^{2}}}}\,\,\,(3)$

Since the temperature distribution determines the density structure, equation (3) can be used to calculate subsidence as a function of time. The elevation e(t) above the final depth to which the lithosphere (which includes the crust) sinks is given, for example, by McKenzie (1978), who proposed

$\displaystyle e\left( t \right)={{E}_{0}}r{{e}^{{-{t}/{\tau }\;}}}\,\,\,(31)$

where

$\displaystyle {{E}_{0}}=\frac{{4a{{\rho }_{{l0}}}\alpha {{T}_{1}}}}{{{{\pi }^{2}}\left( {{{\rho }_{{l0}}}-{{\rho }_{w}}} \right)}}\,\,\,(32)$

and

$\displaystyle r=\left( {\frac{{{{\beta }_{s}}}}{\pi }} \right)\sin \left( {\frac{\pi }{{{{\beta }_{s}}}}} \right)\,\,\,\,(33)$

The thermal subsidence, $\displaystyle \sigma$ (t), since rifting can then be obtained from

$\displaystyle \sigma \left( t \right)=e\left( 0 \right)-e\left( t \right)\,\,\,(34)$

where $\displaystyle \sigma$ (0) is the elevation at t = 0. e(0) is simply E₀r; therefore,

$\displaystyle \sigma \left( t \right)={{E}_{0}}r\left( {1-{{e}^{{-{t}/{\tau }\;}}}} \right)\,\,\,(35)$

A plot of $\displaystyle \sigma$ versus (1 – $\displaystyle {{e}^{{{{-t}}/{\tau }\;}}}$ ) will have a slope of E₀r. This function depends on thermal parameters of the lithosphere as well as $\displaystyle {{\beta }_{s}}$ , the amount of extension. Since $\displaystyle \sigma$ can be estimated from either Airy or flexural backstripping, the slope can be used to estimate $\displaystyle {{\beta }_{s}}$ directly. This procedure has now been used to quantitatively estimate the amount of extension at a number of rift-type basins in various tectonic settings.

3. Continental lithosphere and heat flow provinces

Continental heat flow is harder to understand than oceanic heat flow and harder to fit into a general theory of thermal evolution of the continents or of the Earth. Continental heat-flow values are affected by many factors, including erosion, deposition, glaciation, the length of time since any tectonic events, local concentrations of heat-generating elements in the crust, the presence or absence of aquifers and the drilling of the hole in which the measurements were made. Nevertheless, it is clear that the measured heat-flow values decrease with increasing age. This suggests that, like the oceanic lithosphere, continental lithosphere is cooling and slowly thickening with time.

In some specific areas, there is a linear relationship between surface heat flow and surface radioactive heat generation. Using this relationship, one can make an approximate estimate of the contribution of the heat-generating elements in the continental crust to the surface heat flow. In these areas, the surface heat flow Q₀ can be expressed in terms of the measured surface radioactive heat generation A₀ as

$\displaystyle {{Q}_{0}}={{Q}_{r}}+{{A}_{0}}D\,\,\,(36)$

where Q_r is a constant component of heat flow from the mantle and D represents a depth scale for the vertical distribution of heat-producing elements. A reliable consistency in parameter D at some interval of depths, typically between 10 and 15 km, led workers to define a heat flow province as a region of common tectonothermal history within which consistent values of Q_r and D are obtained. Much effort has been expended in identifying and quantifying heat flow provinces around the world. Several regional correlations are given in Figure 3. In each case, the corresponding length scale D is the slope of the best-fit straight line and the reduced heat flow Q_r is the vertical intercept of the line. These data are summarized in Table 2. Note that in each case a linear correlation appears to fit the data quite well. In all cases the length scale is near 10 km and the reduced heat flow Q_r in general appears to be consistent with the range quoted in Pasquale et al. (2014), who suggest Q_r values ranging from 18 mW/m² for Precambrian areas to 45 mW/m² for Cenozoic areas.

Figure 3. Dependence of surface heat flow Q₀ on radiogenic heat production A₀ per unit volume in surface rock for selected geological provinces: Sierra Nevada (solid squares and very long dashed line), eastern US (solid circles and intermediate dashed line), Norway and Sweden (open circles and solid line), eastern Canadian shield (open squares and short dashed line). In each case the data are fit with the linear relationship (36).

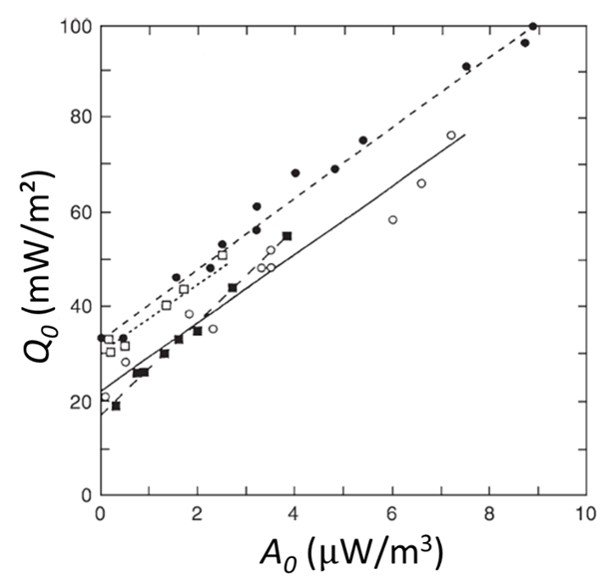
Table 2. Coefficients for linear fit equations shown in Figure 3.

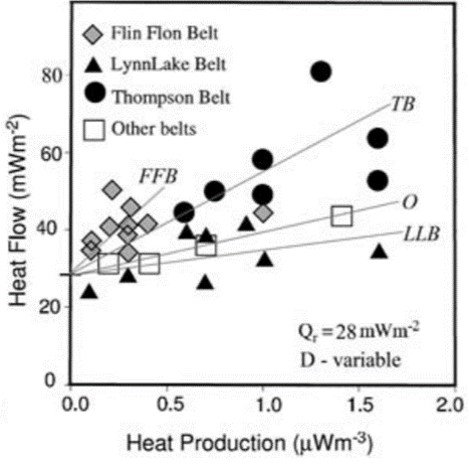
Although equation (36) provides a convenient, simplified description of the thermal structure of continental lithosphere, several objections have been raised over its validity in specific situations. For one, models involving heat-flow provinces often lump together regions and belts with clearly distinct origins and lithologies. Artemieva (2011) mentions the Paleoproterozoic Trans-Hudson Orogen (the central Canadian shield) as an example. The orogen is formed by markedly different structures: the Flin Flon Belt is made up of arc volcanic and plutonic rocks; the Lynn Lake Belt is formed by island arc volcanic rocks; the Thompson Nickel Belt contains metasedimentary rocks; other domains are made up of Archean gneisses. While a single correlation could be suggested for the entire orogen, heat data gathered for individual regions suggest that at least parameter D should be treated as variable from one belt to the next, as illustrated in Figure 4.

Figure 4. Heat-flow province fits for regions of the central Canadian shield.

The second main issue in the heat-province linear equation concerns the fact that it is an effectively 1D treatment and that the scatter around data is, in part, caused by 2D and 3D heat flow effects that smooth lateral variations in heat production. The effect of horizontal variations in heat production in the crust on surface heat flow and thus on the Q–A₀ relationship was examined by harmonic (Jaupart, 1983) and random (Vasseur and Singh, 1986) lateral distributions of heat sources in the crust with a constant or exponential vertical distribution. Those workers found that, in general, lateral flow smoothes variations in heat production so that only shallow anomalies are well reflected in surface heat flow. In almost all cases, lateral heat flow results in an apparently lower D-value as obtained from the heat flow-heat production plot than the actual thickness of the radioactive layer. The amplitude of this reduction depends on the radial distance over which the (randomly distributed) heat production is correlated. If the thickness of the radioactive D-layer is much smaller than the scale of horizontal fluctuations in radioactivity, vertical heat flow prevails and the effect of lateral heat production heterogeneity on Q and on the linear correlation (36) is insignificant. If, however, the scale of horizontal fluctuations is small compared to D, the contribution of lateral heat flow to surface heat flow variations becomes important (Vasseur and Singh, 1986).

Let’s close this article with a simple applied example.

Example

Suppose that, in the eastern United States, a heat flow province can be represented by the usual equation

$\displaystyle Q={{Q}_{r}}+{{A}_{0}}D$

Data from the US Geological Survey suggest that the local lithosphere can be approximated by a heat flow province equation with constants Q_r = 34 mW/m² and D = 7.2 km. Assuming a simple, steady-state, two-layer model of heat production, an average surface temperature of 12^oC, an average thermal conductivity of 2.8 W/mK, and a measured surface heat generation of 3.2 W/m³, what is the temperature, T, at the base of the heat-generation layer?

The linear relationship tells us that surface heat flow

$\displaystyle {{Q}_{0}}=34+3.2\times 7.2=57.0\,\,\text{mW/}{{\text{m}}^{2}}$

and the two-layer model tells us that heat flow decreases linearly with depth to Q_r = 34 mW/m² at 7.2 km. The thermal gradient ( $\displaystyle \partial$ T/ $\displaystyle \partial$ z = Q/k) therefore decreases linearly with depth from 57.0/2.8 = 20.36^oC/km at the surface to 34/2.8 = 12.14^oC/km at 7.2 km; fitting these two data points to a linear equation gives $\displaystyle \partial$ T/ $\displaystyle \partial$ z = 20.36 – 1.142z. Integrating this relation with respect to z brings to

$\displaystyle \frac{{\partial T}}{{\partial z}}=20.36-1.142z\to T\left( z \right)=-0.571{{z}^{2}}+20.36z+C$

As a boundary condition, T(0) = 12^oC, giving

$\displaystyle T\left( 0 \right)=-0.571\times {{0}^{2}}+20.36\times 0+C=12$

$\displaystyle \therefore C=12$

Finally, the temperature profile is given by

$\displaystyle T\left( z \right)=12+20.36z-0.571{{z}^{2}}$

and the temperature at z = 7.2 km is

$\displaystyle T\left( {7.2} \right)=12+20.36\times 7.2-0.571\times {{7.2}^{2}}=129{}^\text{o}\text{C}\leftarrow$

References

• ARTEMIEVA, I. (2011). The Lithosphere: An Interdisciplinary Approach. Cambridge: Cambridge University Press.

• BEARDSMORE, G. and CULL, J. (2001). Crustal Heat Flow. Cambridge: Cambridge University Press.

• Jaupart, C. (1983). Horizontal heat transfer due to radioactivity contrasts: causes and consequences of the linear heat flow relation. Geophys. J. Roy. Astron. Soc., 75, 411 – 435.

• McKenzie, D. (1978). Some remarks on the development of sedimentary basins. Earth Planet. Sci. Lett., 40, 25 – 32.

• PASQUALE, V., VERDOYA, M. and CHIOZZI, P. (2014). Geothermics: Heat Flow in the Lithosphere. Berlin/Heidelberg: Springer.

• Stein, C. and Stein, S. (1992). A model for the global variation in oceanic depth and heat flow with lithospheric age. Nature, 359, 123 – 128.

Heat Flow and Rifting in the Lithosphere: Oceanic and Continental

Subscribe to our Mailing List!

Featured Posts

A Primer on NAND Flash Memories

Solidification Time and Chvorinov’s Rule

Step-Growth Polymerization, the Carothers Equation, and the Flory-Schulz Distribution

More Articles

Stomatal Conductance and Plant Transpiration

Four Models for One-Dimensional Infiltration of Water in Soils

Fields of Study

More

© 2024 Montogue Quiz

Subscribe to
our Mailing List!

Subscribe to our Mailing List!

Subscribe to receive our latest materials in your inbox.

Homework Help

© 2024 Montogue Quiz

Subscribe to our Mailing List!