Droplet Evaporation and Combustion

Droplet evaporation and combustion are the underlying processes of any technical spray application. The major objective of fuel-drop vaporization/combustion studies is to develop simple and accurate models for use in spray analysis involving a large number of droplets. In this post, we develop simple models for droplet evaporation and burning as discussed in Mukhopadhyay and Sen (2019), Turns (2013), and Glassman (1987).

1. Droplet evaporation based on species balance

We begin by developing a simple model for spherical droplet evaporation. Following Mukhopadhyay and Sen (2019), several simplifications are adopted to make the analysis mathematically tractable, namely:

Relative motion between the liquid droplet and the surrounding gas phase is neglected, which means that the droplet is evaporating in a quiescent medium.
The liquid phase has much greater inertia than the vapor phase, so that processes in the vapor phase have a much shorter timescale than their liquid phase counterpart. This enables us to assume that the evaporation process is quasi-steady.
The droplet consists of a single component. Also, the surrounding gaseous medium does not dissolve in the droplet, which may not hold true at very high pressures. This assumption may also break down for alcohol droplets that incorporate moisture from the surrounding air.
The droplet temperature is assumed to be uniform. This assumption eliminates the need to solve the transport equations within the liquid phase. It is reasonable for small droplets, but may not hold true for larger ones.
The initial heat-up period of the droplet is neglected, and the droplet is assumed to be at the boiling point of the liquid.
Mass transfer is controlled by Fickian diffusion.
Radiation heat transfer is negligible.

Figure 1. An evaporating droplet in a quiescent medium.

Given the assumptions above, the transport process can be described by a steady, one-dimensional, spherically symmetric model. Accordingly, we describe the evaporating droplet with a mass-conservation equation,

$\displaystyle \frac{d}{{dr}}\left( {{{\rho }_{l}}{{u}_{r}}A} \right)=0\,\,\,(1)$

where $\displaystyle {{\rho }_{l}}$ is the density of the liquid droplet, u_r is radial velocity, and A is surface area. Noting that A = 4 $\displaystyle \pi$ r² for a sphere, where r is radius, we may write

$\displaystyle {{\rho }_{l}}{{r}^{2}}{{u}_{r}}=\frac{{\dot{m}}}{{4\pi }}=\text{const}\text{.}\,\,\,\text{(2)}$

where $\displaystyle \dot{m}$ is the mass flow rate. We proceed to write an equation for species conservation:

$\displaystyle \frac{d}{{dr}}\left( {{{\rho }_{l}}{{r}^{2}}{{u}_{r}}{{y}_{F}}-{{r}^{2}}{{\rho }_{g}}{{D}_{g}}\frac{{d{{y}_{F}}}}{{dr}}} \right)=0\,\,\,(3)$

where y_F is the mass fraction of fuel liquid, $\displaystyle {{\rho }_{g}}$ is the density of the gas phase, and D_g is the mass diffusivity from the liquid medium to the surrounding gas. Then, we integrate (3) and note that the total mass flux in the vapor phase is equal to that of the fuel vapor, giving

$\displaystyle \dot{m}{{y}_{F}}-4\pi {{r}^{2}}{{\rho }_{g}}{{D}_{g}}\frac{{d{{y}_{F}}}}{{dr}}=\text{const}\text{.}=\dot{m}\,\,\,(4)$

Rearranging:

$\displaystyle \frac{{d{{y}_{F}}}}{{1-{{y}_{F}}}}=-\frac{{\dot{m}}}{{4\pi {{\rho }_{g}}{{D}_{g}}}}\frac{{dr}}{{{{r}^{2}}}}\,\,\,(5)$

Then, we integrate (5) from r = r_d, where r_d is the initial droplet radius, to r $\displaystyle \to$ $\displaystyle \infty$ . The first boundary condition is

$\displaystyle {{y}_{F}}={{y}_{{F,s}}}\,\,\,\text{when}\,\,\,r={{r}_{d}}$

where y_F,s is the mass fraction of liquid at the surface of the droplet; the second boundary condition is

$\displaystyle {{y}_{F}}={{y}_{{F,\infty }}}\,\,\,\text{when}\,\,\,r\to \infty$

where y_F,_∞ is the mass fraction of liquid in the free stream. Integrating and using the foregoing boundary conditions, we get

$\displaystyle \ln \left( {\frac{{1-{{y}_{{F,s}}}}}{{1-{{y}_{{F,\infty }}}}}} \right)=\frac{{d{{y}_{F}}}}{{1-{{y}_{F}}}}=-\frac{{\dot{m}}}{{4\pi {{\rho }_{g}}{{D}_{g}}{{r}_{d}}}}\,\,\,(6)$

Assuming y_F,_∞ = 0 and solving for mass flow:

$\displaystyle \dot{m}=-4\pi {{\rho }_{g}}{{D}_{g}}{{r}_{d}}\ln \left( {1-{{y}_{{F,s}}}} \right)=4\pi {{\rho }_{g}}{{D}_{g}}{{r}_{d}}\ln \left( {\frac{1}{{1-{{y}_{{F,s}}}}}} \right)\,\,\,(7)$

At this point, we define the Spalding transfer number B_Y,

$\displaystyle {{B}_{Y}}=\frac{{{{y}_{{F,s}}}}}{{1-{{y}_{{F,s}}}}}\,\,\,(8)$

so that (7) can be restated as

$\displaystyle \dot{m}=4\pi {{\rho }_{g}}{{D}_{g}}{{r}_{d}}\ln \left( {1+{{B}_{Y}}} \right)\,\,\,(9)$

Now, the mass of the droplet is of course given by the product of volume and density:

$\displaystyle {{m}_{d}}=\frac{4}{3}\pi r_{d}^{3}{{\rho }_{l}}\,\,\,(10)$

so that, differentiating (10) with respect to time and noting that $\displaystyle \dot{m}$ = d $\displaystyle {{m}_{d}}$ /dt, we have

$\displaystyle \dot{m}=4\pi {{\rho }_{g}}{{D}_{g}}{{r}_{d}}\ln \left( {1+{{B}_{Y}}} \right)=-4\pi {{\rho }_{l}}r_{d}^{2}\frac{{d{{r}_{d}}}}{{dt}}\,\,\,(11)$

or, equivalently:

$\displaystyle \dot{m}=4\pi {{\rho }_{g}}{{D}_{g}}{{r}_{d}}\ln \left( {1+{{B}_{Y}}} \right)=-4\pi {{\rho }_{l}}\frac{d}{{dt}}\left( {\frac{{r_{d}^{2}}}{2}} \right)\,\,\,(12)$

Rearranging, we finally obtain

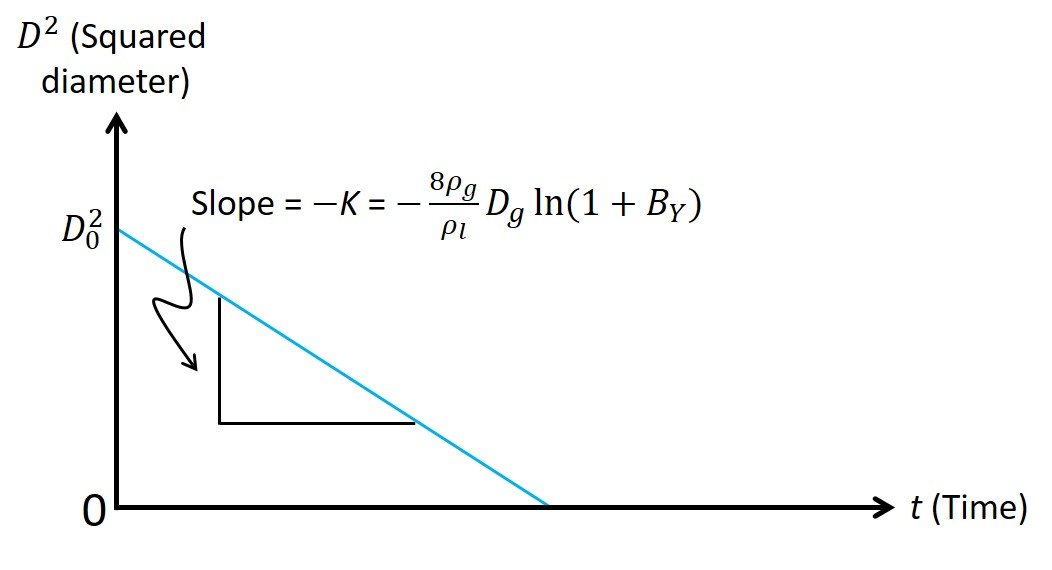
$\displaystyle \frac{d}{{dt}}\left( {{{D}^{2}}} \right)=-8\frac{{{{\rho }_{g}}}}{{{{\rho }_{l}}}}{{D}_{g}}\ln \left( {1+{{B}_{Y}}} \right)=-K\,\,\,(13)$

where we have replaced the droplet radius r_d with its diameter D = 2r_d. Note that, for the problem at hand, all quantities in the middle of (13) remain unchanged over the course of the evaporation process and can be condensed in a parameter K known as the evaporation constant. Equation (13) is an important result, in that it states that the surface area of the droplet, which is proportional to squared diameter, decreases linearly as a function of time, as shown in Figure 2; this relationship is sometimes called the D²–law. That is, the squared diameter of the droplet varies in time t according to the expression

$\displaystyle {{D}^{2}}\left( t \right)=D_{0}^{2}-Kt\,\,\,(14)$

The droplet lifetime – i.e., the time required to evaporate the droplet completely – can be estimated by setting (14) to zero and solving for t:

$\displaystyle {{t}_{d}}=\frac{{D_{0}^{2}}}{K}\,\,\,(15)$

Bear in mind that use of (15) requires knowledge of the fuel concentration at the droplet surface, which appears in the Spalding transfer number B_Y (equation (8)), which in turn appears in the definition of evaporation constant (equation (13)).

Figure 2. The linear relationship between squared diameter and time during droplet evaporation.

2. Droplet evaporation based on energy balance

Note that in deriving equation (13) we have made no use of energy balances, instead relying only upon mass and species conservation. An alternative yet similar assessment of droplet evaporation can be obtained with the energy equation, which for an evaporating droplet reads

$\displaystyle \frac{d}{{dr}}\left( {{{\rho }_{l}}{{r}^{2}}{{u}_{r}}{{c}_{p}}T-{{r}^{2}}k\frac{{dT}}{{dr}}} \right)=\frac{d}{{dr}}\left( {\dot{m}{{c}_{p}}T-4\pi {{r}^{2}}k\frac{{dT}}{{dr}}} \right)=0\,\,\,(16)$

where T is temperature, c_p is the constant-pressure specific heat capacity of the droplet liquid, k is the thermal conductivity of the droplet liquid, and other variables carry the same meaning as in (3). Integrating (16) for conditions at the surface yields

$\displaystyle \dot{m}{{c}_{p}}{{T}_{s}}-4\pi r_{d}^{2}k\frac{{dT\left( {r={{r}_{d}}} \right)}}{{dr}}=0\,\,\,(17)$

where T_s is the temperature at the surface of the droplet. Since the initial heat-up period is neglected and the droplet is at the boiling temperature, all heat supplied from the gas phase to the droplet is latent heat; accordingly, we may write

$\displaystyle 4\pi r_{d}^{2}k\frac{{dT\left( {r={{r}_{d}}} \right)}}{{dr}}=\dot{m}{{h}_{{fg}}}\,\,\,(18)$

where h_fg is the latent heat of evaporation of the droplet. Substituting this into (17) brings to

$\displaystyle \dot{m}\left[ {{{c}_{p}}\left( {T-{{T}_{s}}} \right)+{{h}_{{fg}}}} \right]=4\pi {{r}^{2}}k\frac{{dT}}{{dr}}\,\,\,(19)$

This equation can be integrated and manipulated to yield

$\displaystyle \dot{m}=4\pi k{{r}_{d}}\ln \left[ {\frac{{{{c}_{p}}\left( {{{T}_{\infty }}-{{T}_{s}}} \right)+{{h}_{{fg}}}}}{{{{h}_{{fg}}}}}} \right]=4\pi k{{r}_{d}}\ln \left( {1+{{B}_{q}}} \right)\,\,\,(20)$

where T_∞ is the temperature of the quiescent gas medium and

$\displaystyle {{B}_{q}}=\frac{{{{c}_{p}}\left( {{{T}_{\infty }}-{{T}_{s}}} \right)}}{{{{h}_{{fg}}}}}\,\,\,(21)$

is the Spalding transfer number based on heat transfer. Similarly to the derivation based on species conservation, we can define an evaporation constant K such that

$\displaystyle K=-\frac{d}{{dt}}\left( {{{D}^{2}}} \right)=8\frac{k}{{{{\rho }_{l}}{{c}_{p}}}}\ln \left( {1+{{B}_{q}}} \right)\,\,\,(22)$

Equipped with the foregoing equations, computing droplet lifetime is a simple task. However, as noted by Turns (2013), one important issue is how to establish the constant-pressure specific heat capacity c_p and the thermal conductivity k, which are known to vary with temperature and other thermophysical quantities. One simple way to proceed is to take

$\displaystyle {{c}_{p}}={{c}_{{p,F}}}\left( {\bar{T}} \right)\,\,\,(23.1)$

$\displaystyle k=0.4{{k}_{F}}\left( {\bar{T}} \right)+0.6{{k}_{\infty }}\left( {\bar{T}} \right)\,\,\,(23.2)$

where subscripts F and ∞ refer to the droplet liquid and the quiescent medium, respectively, and $\displaystyle \bar{T}$ is the average of the fuel boiling point temperature, T_boil, and that of the free stream, T_∞:

$\displaystyle \bar{T}=\frac{{{{T}_{{\text{boil}}}}+{{T}_{\infty }}}}{2}\,\,\,(23.3)$

Example 1

A 800- $\displaystyle \text{ }\!\!\mu\!\!\text{ }$ m diameter n-octane (C₈H₁₈) droplet is evaporating in a gaseous nitrogen-filled chamber at 1 atm. The N₂ temperature is 600 K. Find the lifetime of the n-octane droplet assuming the droplet temperature is at the boiling point. Take 300 kJ/kg and 703 kg/m³ as the heat of vaporization and density of liquid n-octane, respectively. The normal boiling point of n-octane is approximately 400 K. The thermal conductivity of molecular nitrogen at 500 K is 0.0389 W/m⋅K.

Solution. The boiling point of n-octane is about 400 K, and the free stream temperature is 600 K. Following Turns’ recommended approach, we shall use properties on the basis of a temperature $\displaystyle \bar{T}$ such that

$\displaystyle \bar{T}=\frac{{400+600}}{2}=500\,\text{K}$

Turns’ textbook notes that the constant-pressure specific heat capacity of n-octane ranging from 275 to 755 K can be obtained with the polynomial equation

$\displaystyle {{c}_{p}}\left[ {\text{J/kg}\cdot \text{K}} \right]=2.14\times {{10}^{2}}+5.36T-1.18\times {{10}^{{-3}}}{{T}^{2}}-6.99\times {{10}^{{-7}}}{{T}^{3}}$

$\displaystyle \therefore {{c}_{p}}=2.14\times {{10}^{2}}+5.36\times 500-1.18\times {{10}^{{-3}}}\times {{500}^{2}}-6.99\times {{10}^{{-7}}}\times {{500}^{3}}$

$\displaystyle \therefore {{c}_{{p,F}}}=2512\,\text{J/kg}\cdot \text{K}$

Likewise, the thermal conductivity of n-octane for a temperature ranging from 250 to 500 K is given by

$\displaystyle k\left[ {\text{W/m}\cdot \text{K}} \right]=-4.01\times {{10}^{{-3}}}+3.39\times {{10}^{{-5}}}T+8.19\times {{10}^{{-8}}}{{T}^{2}}$

$\displaystyle \therefore k=-4.01\times {{10}^{{-3}}}+3.39\times {{10}^{{-5}}}\times 500+8.19\times {{10}^{{-8}}}\times {{500}^{2}}$

$\displaystyle \therefore {{k}_{F}}=0.0334\,\text{W/m}\cdot \text{K}$

Further, the thermal conductivity of molecular nitrogen at 500 K is 0.0389 W/mK. We proceed to compute the weighted thermal conductivity (equation (23.2))

$\displaystyle k=0.4\times 0.0334+0.6\times 0.0389=0.0367\,\text{W/m}\cdot \text{K}$

Using (21), we compute the Spalding transfer number:

$\displaystyle {{B}_{q}}=\frac{{2512\times \left( {600-400} \right)}}{{300,000}}=1.67$

Next, we determine the evaporation constant:

$\displaystyle K=8\times \frac{{0.0367}}{{703\times 2512}}\ln \left( {1+1.67} \right)=1.63\times {{10}^{{-7}}}\ {{\text{m}}^{2}}\text{/s}$

Lastly, we compute the droplet lifetime:

$\displaystyle {{t}_{d}}=\frac{{D_{0}^{2}}}{K}=\frac{{{{{\left( {800\times {{{10}}^{{-6}}}} \right)}}^{2}}}}{{1.63\times {{{10}}^{{-7}}}}}=3.93\,\text{s}\leftarrow$

The droplet will be fully vaporized within less than 4 seconds.

3. Droplet burning

Sometimes flames form around individual droplets. In a process of this kind, fuel vapor originating from an individual droplet and oxygen from the surrounding atmosphere undergo a chemical reaction, and a flame is formed at the location where the fuel and the oxidizer are in stoichiometric proportions. From a modelling perspective, a spherically symmetric diffusion flame surrounding a droplet can be represented with equations akin to those of an evaporating droplet; however, the presence of chemical reaction adds thermophysical unknowns to the problem, and more unknowns imply more equations. Over the years, several authors have proposed different formulations of droplet burning with varying degrees of realism and computational complexity; one of the simplest approaches is described in Turns (2013), whose basic results we summarize and exemplify in the remainder of this post.

Our simplified model is based on several assumptions, namely:

The burning droplet is surrounded by a spherically symmetric flame that exists in a quiescent, infinite medium in which convection effects are ignored and neighboring droplets, if there are any, do not interact with each other.
As in our treatment of evaporation, the burning process is quasi-steady.
As in our treatment of evaporation, the droplet consists of a single component. Phase equilibrium between the liquid droplet and the gaseous quiescent medium holds at the liquid-vapor interface.
The pressure is uniform and constant.
The gas phase consists of fuel vapor, oxidizer, and combustion products. The gas-phase region is divided into two zones. There is an inner zone between the droplet surface and the flame, which contains only fuel vapor and products; and an outer zone that consists of oxidizer and products. Binary diffusion prevails in each region.
As mentioned above, fuel and oxidizer occur in stoichiometric proportions at the flame. An infinite reaction rate is assumed, which implies that the flame is infinitely thin.
The Lewis number (i.e., the ratio of thermal diffusivity to mass diffusivity) equals unity.
Radiation heat transfer is negligible.

Formulating the burning droplet model and solving the ensuing equations, we obtain the following results. First, the burning rate is given by

$\displaystyle {{\dot{m}}_{F}}=\frac{{4\pi k{{r}_{s}}}}{{{{c}_{p}}}}\ln \left[ {1+\frac{{{{\Delta {{h}_{c}}}}/{{v+{{c}_{p}}\left( {{{T}_{\infty }}-{{T}_{s}}} \right)}}\;}}{{{{q}_{{i-l}}}+{{h}_{{fg}}}}}} \right]\,\,\,(24)$

where subscript F denotes ‘fuel’, k is thermal conductivity of the gas phase, r_s is the droplet radius at the liquid-vapor interface, c_p is constant-pressure specific heat capacity of the gas phase, T_∞ is the free-stream temperature, T_s is the droplet surface temperature, v is the stoichiometric air-fuel ratio, $\displaystyle \Delta$ h_c is the heat of combustion of the fuel, h_fg is the heat of vaporization of the fuel, and q_i-l is the heat conducted into the droplet interior, which can be treated in several ways, as discussed in Turns’ textbook; with negligible thermal inertia, q_i-l = 0. The equation above can be simplified if we define the transfer number for a burning droplet, $\displaystyle {{\beta }_{q}}$ , namely

$\displaystyle {{\beta }_{q}}=\frac{{{{\Delta {{h}_{c}}}}/{v}\;+{{c}_{p}}\left( {{{T}_{\infty }}-{{T}_{s}}} \right)}}{{{{q}_{{i-l}}}+{{h}_{{fg}}}}}\,\,\,(25)$

so that (24) can be restated as

$\displaystyle {{\dot{m}}_{F}}=\frac{{4\pi k{{r}_{s}}}}{{{{c}_{p}}}}\ln \left( {1+{{\beta }_{q}}} \right)\,\,\,(26)$

which is akin to (20) for droplet evaporation without chemical reaction.

Another parameter that can be readily obtained from the model is the flame radius r_f:

$\displaystyle {{r}_{f}}={{r}_{s}}\frac{{\ln \left( {1+{{\beta }_{q}}} \right)}}{{\ln \left[ {{{\left( {v+1} \right)}}/{v}\;} \right]}}\,\,\,(27)$

Dividing both sides by r_s gives the stand-off ratio r_f/r_s.

Also useful is the flame temperature, T_f:

$\displaystyle {{T}_{f}}={{T}_{s}}+\frac{{{{q}_{{i-l}}}+{{h}_{{fg}}}}}{{{{c}_{p}}\left( {1+v} \right)}}\left( {v{{\beta }_{q}}-1} \right)\,\,\,(28)$

We may also compute the fuel mass fraction at the droplet surface:

$\displaystyle {{y}_{{F,s}}}=\frac{{{{\beta }_{q}}-{1}/{v}\;}}{{{{\beta }_{q}}+1}}\,\,\,(29)$

The droplet mass burning rate in terms of the transfer number, $\displaystyle {{\beta }_{q}}$ , is of similar form to the expression derived for the evaporation rate (equation (22)). Accordingly, without further development, we can define the so-called burning rate constant as

$\displaystyle \kappa =8\frac{k}{{{{\rho }_{l}}{{c}_{p}}}}\ln \left( {1+{{\beta }_{q}}} \right)\,\,\,(30)$

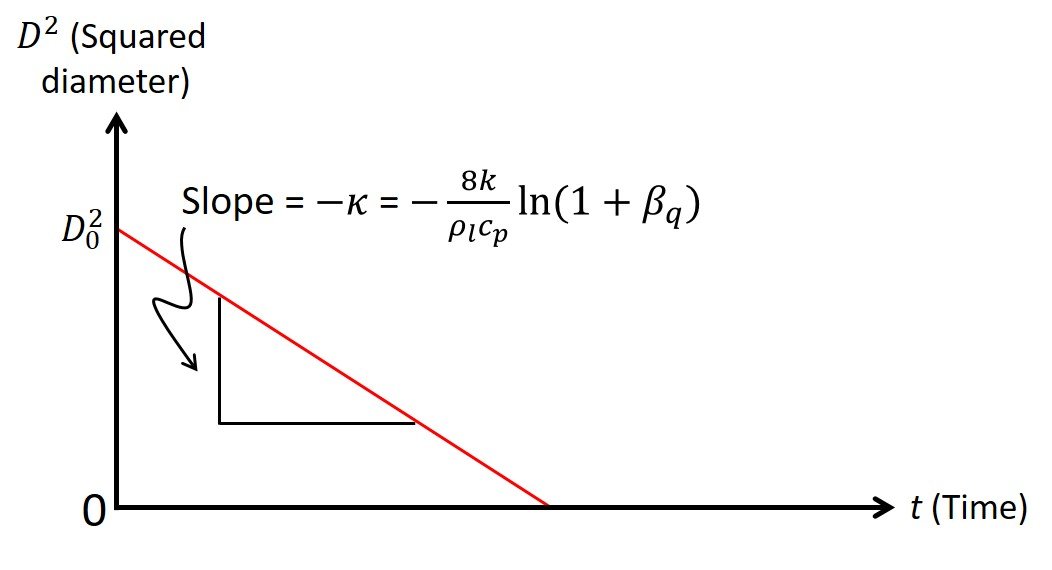
where $\displaystyle {{\rho }_{l}}$ is the density of the liquid fuel. Importantly, the burning rate constant is truly a constant only after a steady-state surface temperature is achieved, which is a requirement for $\displaystyle {{\beta }_{q}}$ to be a constant. Assuming that the transient heat-up period is small in comparison with the droplet lifetime, we can write a D²-law for droplet burning (Figure 3):

$\displaystyle {{D}^{2}}\left( t \right)=D_{0}^{2}-\kappa t\,\,\,(31)$

Moreover, the droplet lifetime can be obtained by setting (31) to zero and solving for time:

$\displaystyle {{t}_{d}}=\frac{{D_{0}^{2}}}{\kappa }\,\,\,(32)$

Figure 3. Linear relationship between squared diameter and time during droplet burning.

As in the case of droplet evaporation, assessment of droplet burning requires appropriate values of the constant-pressure specific heat, c_p, thermal conductivity, k, and liquid density, $\displaystyle {{\rho }_{l}}$ . Following Turns’ recommendations, we may take

$\displaystyle {{c}_{p}}={{c}_{{p,F}}}\left( {\bar{T}} \right)\,\,\,(33.1)$

$\displaystyle k=0.4{{k}_{F}}\left( {\bar{T}} \right)+0.6{{k}_{{Ox}}}\left( {\bar{T}} \right)\,\,\,(33.2)$

$\displaystyle {{\rho }_{l}}={{\rho }_{l}}\left( {{{T}_{s}}} \right)\,\,\,(33.3)$

where subscripts F and Ox refer to the droplet fuel and the oxidizer, respectively, and $\displaystyle \bar{T}$ is the average of the temperature at the surface of the droplet, T_s, and the flame temperature, T_f:

$\displaystyle \bar{T}=\frac{{{{T}_{\text{s}}}+{{T}_{f}}}}{2}\,\,\,(33.4)$

Example 2

Consider the combustion of an n-octane (C₈H₁₈) droplet with diameter equal to 800 $\displaystyle \text{ }\!\!\mu\!\!\text{ }$ m. The quiescent medium is air at 300 K. Compute the fuel flow rate, the stand-off ratio, the flame radius, the fuel mass fraction at the droplet surface, and the droplet lifetime. The flame temperature may be taken to be about 2200 K. The heat of evaporation and the heat of combustion for n-octane are given as h_fg = 300 kJ/kg and $\displaystyle \Delta$ h_c = 44,790 kJ/kg, respectively. Also, use equation (28) to check if this assumed flame temperature is reasonable.

Solution. The average temperature we shall use as a reference is, resorting to (33.4):

$\displaystyle \bar{T}=\frac{{{{T}_{s}}+{{T}_{f}}}}{2}=\frac{{400+2200}}{2}=1300\,\text{K}$

The constant-pressure specific heat capacity of n-octane in the range of temperatures from 755 to 1365 K can be estimated with the polynomial equation

$\displaystyle {{c}_{p}}\left[ {\text{J/kg}\cdot \text{K}} \right]=2.44\times {{10}^{3}}-4.47T+1.67\times {{10}^{{-2}}}{{T}^{2}}-1.79\times {{10}^{{-5}}}{{T}^{3}}+8.64\times {{10}^{{-9}}}{{T}^{4}}-1.61\times {{10}^{{-12}}}{{T}^{5}}$

$\displaystyle \therefore {{c}_{p}}=2.44\times {{10}^{3}}-4.47\times 1300+1.67\times {{10}^{{-2}}}\times {{1300}^{2}}-1.79\times {{10}^{{-5}}}\times {{1300}^{3}}+8.64\times {{10}^{{-9}}}\times {{1300}^{4}}-1.61\times {{10}^{{-12}}}\times {{1300}^{5}}$

$\displaystyle \therefore {{c}_{p}}=4225\,\text{J/kg}\cdot \text{K}=\text{4}\text{.225}\,\text{kJ/kg}\cdot \text{K}$

The thermal conductivity of air at 1300 K is 0.082 W/m⋅K, whereas that of n-octane could be determined with the same polynomial equation we’ve employed in the evaporation example,

$\displaystyle k\left[ {\text{W/m}\cdot \text{K}} \right]=-4.01\times {{10}^{{-3}}}+3.39\times {{10}^{{-5}}}T+8.19\times {{10}^{{-8}}}{{T}^{2}}$

but this correlation only covers the temperature range from 250 to 500 K. One easy way to circumvent this problem is take the thermal conductivity at the highest temperature for which this expression holds (k = 0.0334 W/m⋅K at T = 500 K) and use the fact that thermal conductivity approximately scales with temperature to the 1/2 power:

$\displaystyle {{k}_{F}}\left( {\bar{T}} \right)=\left[ {{{k}_{F}}\left( {500\,\text{K}} \right)} \right]\times {{\left( {\frac{{\bar{T}}}{{500}}} \right)}^{{{1}/{2}\;}}}$

$\displaystyle \therefore {{k}_{F}}\left( {\bar{T}} \right)=0.0334\times {{\left( {\frac{{1300}}{{500}}} \right)}^{{{1}/{2}\;}}}=0.0539\,\text{W/m}\cdot \text{K}$

The thermal conductivity is then given by the weighted estimate

$\displaystyle k=0.4{{k}_{F}}\left( {\bar{T}} \right)+0.6{{k}_{{Ox}}}\left( {\bar{T}} \right)$

$\displaystyle \therefore k=0.4\times 0.0539+0.6\times 0.082=0.0708\,\text{W/m}\cdot \text{K}$

Next, we compute the stoichiometric air-fuel ratio, noting that for n-octane x = 8, y =18, and that the average ‘molar’ mass of air is 28.85 g/mol:

$\displaystyle v=\left( {x+{y}/{4}\;} \right)4.76\frac{{M{{W}_{{Ox}}}}}{{M{{W}_{F}}}}=\left( {8+{{18}}/{4}\;} \right)\times 4.76\times \frac{{28.85}}{{114}}=15.06$

Also, the heat of evaporation and the heat of combustion for n-octane are given as h_fg = 300 kJ/kg and $\displaystyle \Delta$ h_c = 44,790 kJ/kg, respectively. We proceed to compute the transfer number $\displaystyle {{\beta }_{q}}$ ,

$\displaystyle {{\beta }_{q}}=\frac{{{{\Delta {{h}_{c}}}}/{{v+{{c}_{p}}\left( {{{T}_{\infty }}-{{T}_{s}}} \right)}}\;}}{{{{q}_{{i-l}}}+{{h}_{{fg}}}}}$

$\displaystyle \therefore {{\beta }_{q}}=\frac{{{{44,790}}/{{15.06+4.225\times \left( {300-400} \right)}}\;}}{{0+300}}=8.51$

where we have ignored droplet heating so that q_i-l = 0. We now have all the information needed to compute the mass burning rate (equation (26)):

$\displaystyle {{\dot{m}}_{F}}=\frac{{4\pi k{{r}_{s}}}}{{{{c}_{p}}}}\ln \left( {1+{{\beta }_{q}}} \right)$

$\displaystyle \therefore {{\dot{m}}_{F}}=\frac{{4\pi \times 0.0708\times \left( {400\times {{{10}}^{{-6}}}} \right)}}{{4225}}\ln \left( {1+8.51} \right)=1.90\times {{10}^{{-7}}}\,\text{kg/s}$

$\displaystyle \therefore {{\dot{m}}_{F}}=0.19\,\text{mg/s}\leftarrow$

The flame stand-off ratio is determined next (equation (27)):

$\displaystyle \frac{{{{r}_{f}}}}{{{{r}_{d}}}}=\frac{{\ln \left( {1+{{\beta }_{q}}} \right)}}{{\ln \left[ {{{\left( {v+1} \right)}}/{v}\;} \right]}}=\frac{{\ln \left( {1+8.51} \right)}}{{\ln \left[ {{{\left( {15.06+1} \right)}}/{{15.06}}\;} \right]}}=35.0\leftarrow$

which means that the flame radius is 35 times the initial radius of the droplet, or 35 $\displaystyle \times$ 400 = 14,000 $\displaystyle \text{ }\!\!\mu\!\!\text{ }$ m = 14 mm. Now, the flame temperature can be estimated with equation (28):

$\displaystyle {{T}_{f}}={{T}_{s}}+\frac{{{{q}_{{i-l}}}+{{h}_{{fg}}}}}{{{{c}_{p}}\left( {1+v} \right)}}\left( {v{{\beta }_{q}}-1} \right)$

$\displaystyle \therefore {{T}_{f}}=400+\frac{{0+300}}{{4.225\times \left( {1+15.06} \right)}}\left( {15.06\times 8.51-1} \right)=962.2\,\text{K}\leftarrow$

There is large disagreement between our estimate and the assumed flame temperature of 2200 K. Turns (2013) notes that this deviation should be attributed not to our guess, but to the underlying theory; specifically, our specific heat capacity c_p $\displaystyle \approx$ 4.2 kJ/kg⋅K is probably a substantial overestimate.

The fuel mass fraction at the droplet surface is, in turn (equation (29)):

$\displaystyle {{y}_{{F,s}}}=\frac{{{{\beta }_{q}}-{1}/{v}\;}}{{{{\beta }_{q}}+1}}$

$\displaystyle {{y}_{{F,s}}}=\frac{{8.51-{1}/{{15.06}}\;}}{{8.51+1}}=0.888\leftarrow$

We proceed to compute the burning rate constant (equation (30)),

$\displaystyle \kappa =8\frac{k}{{{{\rho }_{l}}{{c}_{p}}}}\ln \left( {1+{{\beta }_{q}}} \right)=8\times \frac{{0.0708}}{{703\times 4225}}\ln \left( {1+8.51} \right)=4.30\times {{10}^{{-7}}}\,{{\text{m}}^{2}}\text{/s}$

and, finally, the droplet lifetime (equation (32)):

$\displaystyle {{t}_{d}}=\frac{{D_{0}^{2}}}{\kappa }=\frac{{{{{\left( {800\times {{{10}}^{{-6}}}} \right)}}^{2}}}}{{4.30\times {{{10}}^{{-7}}}}}=1.49\,\text{s}\leftarrow$

The droplet will be fully burned within approximately 1.5 seconds.

References

GLASSMAN, I. (1987). Combustion. 2nd edition. London: Academic Press.
MUKHOPADHYAY, A. and SEN, S. (2019). Fundamentals of Combustion Engineering. Boca Raton: CRC Press.
TURNS, S.R. (2013). An Introduction to Combustion: Concepts and Applications. 3rd edition. New York: McGraw-Hill.

Droplet Evaporation and Combustion

Subscribe to our Mailing List!

Featured Posts

A Primer on NAND Flash Memories

Solidification Time and Chvorinov’s Rule

Step-Growth Polymerization, the Carothers Equation, and the Flory-Schulz Distribution

More Articles

Vertical-Axis Wind Turbines

Plasticity: Tresca and von Mises Yield Criteria

Fields of Study

More

© 2024 Montogue Quiz

Subscribe to
our Mailing List!

Subscribe to our Mailing List!

Subscribe to receive our latest materials in your inbox.

Homework Help

© 2024 Montogue Quiz

Subscribe to our Mailing List!