Plasticity: Tresca and von Mises Yield Criteria

1. Yield Surfaces

Plasticity theory is the study of structural strains beyond the linear region in which deformations are elastic and Hooke’s law describes mechanical behavior. The existence of a fixed region of admissible generalized stresses is a key concept in this field.

When modelling elastic-plastic behavior, it is assumed that at all times, the generalized stress lies in a closed, connected set S of admissible generalized stresses (Figure 1). The interior of this set is called the elastic region and may be denoted as $\displaystyle E$ . The boundary of S is denoted by $\displaystyle B$ and is known as the yield surface. The region S^c (that is, the complement of the region of admissible stresses) is not physically attainable.

The significance of an elastic region is that purely elastic behavior occurs when the generalized strain-stress combination is contained within $\displaystyle E$ or when the generalized stress moves from $\displaystyle B$ to the interior of S (elastic unloading). Plastic behavior takes place only if generalized stress lies on the yield surface and, after some mechanical adjustment, continues to lie on the yield surface; this is known as plastic loading.

Various criteria have been suggested in the past to predict the yielding of metals and other ductile materials under complex stress fields. However, most of them precede the now widely accepted finding, brought about by extensive theoretical and experimental work in the first half of the 20th century, that hydrostatic stress has no effect on yielding. Two of the oldest surviving criteria in modern plasticity are those due to Tresca and von Mises, which we briefly discuss below.

Figure 1. A hypothetical yield locus.

2. Tresca yield criterion

The Tresca yield criterion was first presented by French mechanical engineer Henri Tresca (1814 – 1885) in 1864. In this model, yielding will begin to occur once one-half of the largest difference between the principal stresses reaches a certain critical value k. In mathematical terms, we can state the criterion as

$\displaystyle \text{For}\,\,\text{onset of yielding: }\frac{1}{2}\left( {{{\sigma }_{{\max }}}-{{\sigma }_{{\min }}}} \right)={{k}_{T}}\,\,\,\,\,\mathbf{(1)}$

where $\displaystyle {{\sigma }_{{\max }}}$ and $\displaystyle {{\sigma }_{{\min }}}$ indicate the algebraic maximum and minimum values of the principal stresses, respectively. In turn, k_T is the critical stress that defines the criterion; it is closely related to the loading conditions to which a mechanical specimen is subjected. If pure shear is used, then k_T is the shear yield stress k_G Alternatively, one may appeal to a simple tensile test, so that the maximum principal stress is the normal yield stress Y and the minimum principal stress is zero, giving

$\displaystyle \frac{1}{2}\left( {Y-0} \right)={{k}_{T}}$

$\displaystyle \therefore {{k}_{T}}=\frac{Y}{2}\,\,\,\,\,\mathbf{(2)}$

Note that comparing k_T = k_G in pure shear conditions with k_T = Y/2 in uniaxial tensile conditions leads to the interesting relationship

$\displaystyle {{k}_{G}}=\frac{Y}{2}\,\,\,\,\,\mathbf{(3)}$

which indicates that, under ideal Tresca yielding behavior, the yield stress for pure shear, k_G, is simply half of the yield stress for pure tension, Y. Of course, the mathematical relationship between these two parameters is usually not so straightforward; it follows that k_T in real materials has no absolute definition, and is possibly stress-state dependent to some degree (Shames and Cozzarelli, 1997). In modern plasticity modeling, data derived from uniaxial tensile tests seem preferable to those obtained with pure shear analysis, so using k_T = Y/2 is more common.

Thus, to ascertain whether we have yielding at a point for a given state of stress, one may compare the quantity

$\displaystyle \text{ }\frac{1}{2}\left( {{{\sigma }_{{\max }}}-{{\sigma }_{{\min }}}} \right)\,\,\,\,\,\mathbf{(4)}$

and the quantity Y/2 resulting from a one-dimensional tensile test of the same material at yielding. If

$\displaystyle \text{ }\frac{1}{2}\left( {{{\sigma }_{{\max }}}-{{\sigma }_{{\min }}}} \right)<\frac{Y}{2}\,\,\,\,\,\left( \mathbf{5} \right)$

we have elastic behavior; on the other hand, if

$\displaystyle \text{ }\frac{1}{2}\left( {{{\sigma }_{{\max }}}-{{\sigma }_{{\min }}}} \right)\ge \frac{Y}{2}\,\,\,\,\,\left( \mathbf{6} \right)$

we can expect yielding per the Tresca criterion.

3. Von Mises yield criterion and the principal stress form

The von Mises criterion is named after Richard von Mises (1883 – 1953), an Austrian professor of mechanics and applied mathematics who taught at prestigious schools, most notably Harvard University. In a seminal 1913 paper, Mises suggested, from purely theoretical considerations, that yielding occurs when J₂, the second invariant of the stress deviator tensor, attains a critical value $\displaystyle k_{M}^{2}$ such that

$\displaystyle {{J}_{2}}=k_{M}^{2}=\frac{{{{Y}^{2}}}}{3}\,\,\,\,\,\left( \mathbf{7} \right)$

where Y is the normal yield stress.

While the second stress invariant approach is mathematically meaningful and constitutes the technique initially adopted by von Mises, there exist other interpretations of the yield criterion at issue. The best one, arguably, is the energy-based explanation provided by German engineer Heinrich Hencky (1885 – 1951) in the 1920s. Hencky’s interpretation relies on the continuum-mechanical decomposition of total strain energy into a dilatational (volumetric) component and a distortional (shear) component. The former depends upon the mean, or hydrostatic, component of the applied stress and the latter upon the remaining reduced, or deviatoric, component of stress, as illustrated in Figure 2. Hencky posited that plastic deformation ensues when the deviatoric strain energy, associated with the shape change of a material element, reaches a critical value determined experimentally from a uniaxial tension test. The notion that the onset of plastic deformation is attributed to distortional energy has the crucial implication that hydrostatic stress, which only produces energy of volume change in isotropic materials, does not cause yielding.

Figure 2. Decomposing total stress.

3.1. Quick derivation of the von Mises criterion (normal form).

In Fig. 2, the total strain energy may be determined with the integral

$\displaystyle U=\int{{\sigma d\varepsilon }}=\int{{\left( {{{\sigma }_{1}}d{{\varepsilon }_{1}}+{{\sigma }_{2}}d{{\varepsilon }_{2}}+{{\sigma }_{3}}d{{\varepsilon }_{3}}} \right)}}\,\,\,\,\,\left( \mathbf{8} \right)$

But, by the constitutive relations

$\displaystyle {{\varepsilon }_{1}}=\frac{1}{E}\left[ {{{\sigma }_{1}}-\nu \left( {{{\sigma }_{2}}+{{\sigma }_{3}}} \right)} \right]$

$\displaystyle {{\varepsilon }_{2}}=\frac{1}{E}\left[ {{{\sigma }_{2}}-\nu \left( {{{\sigma }_{1}}+{{\sigma }_{3}}} \right)} \right]\,\,\,\,\,\mathbf{(9}-\mathbf{11)}$

$\displaystyle {{\varepsilon }_{3}}=\frac{1}{E}\left[ {{{\sigma }_{3}}-\nu \left( {{{\sigma }_{1}}+{{\sigma }_{2}}} \right)} \right]$

where E is Young’s modulus and $\displaystyle \nu$ is Poisson’s ratio, we substitute in (8) and carry out the integration, giving

$\displaystyle U=\frac{1}{{2E}}\left( {\sigma _{1}^{2}+\sigma _{2}^{2}+\sigma _{3}^{2}} \right)-\frac{\nu }{E}\left( {{{\sigma }_{1}}{{\sigma }_{2}}+{{\sigma }_{2}}{{\sigma }_{3}}+{{\sigma }_{1}}{{\sigma }_{3}}} \right)\,\,\,\left( {\mathbf{12}} \right)$

In turn, the volumetric strain energy density arises from the hydrostatic component of stress (see Figure 2), namely

$\displaystyle {{U}_{V}}=\int{{\sigma d\varepsilon }}=\int{{\left( {{{\sigma }_{m}}d\varepsilon +{{\sigma }_{m}}d\varepsilon +{{\sigma }_{m}}d\varepsilon } \right)}}\,\,\,\,\,\left( {\mathbf{13}} \right)$

Substituting $\displaystyle \varepsilon$ = $\displaystyle {{\sigma }_{m}}$ /3K for the linear strain along an edge, where K is the bulk modulus,

$\displaystyle {{U}_{V}}=\int{{3{{\sigma }_{m}}d\varepsilon }}=\int{{3{{\sigma }_{m}}\frac{{d{{\sigma }_{m}}}}{{3K}}}}=\frac{{\sigma _{m}^{2}}}{{2K}}\,\,\,\,\,\left( {\mathbf{14}} \right)$

But E = 2K(1 – 2 $\displaystyle \nu$ ), thus

$\displaystyle {{U}_{V}}=\frac{{\sigma _{m}^{2}}}{{2K}}=\frac{{3\left( {1-2\nu } \right)\sigma _{m}^{2}}}{{2E}}\,\,\,\,\,\left( {\mathbf{15}} \right)$

Using $\displaystyle {{\sigma }_{m}}$ = $\displaystyle {{\sigma }_{{kk}}}$ /3,

$\displaystyle {{U}_{V}}=\frac{{3\left( {1-2\nu } \right)\sigma _{m}^{2}}}{{2E}}=\frac{{\left( {1-2\nu } \right){{{\left( {{{\sigma }_{1}}+{{\sigma }_{2}}+{{\sigma }_{3}}} \right)}}^{2}}}}{{6E}}\,\,\,\left( {\mathbf{16}} \right)$

Subtracting (16) from (12) gives the strain energy associated with the deviatoric stress,

$\displaystyle {{U}_{S}}=U-{{U}_{V}}$

$\displaystyle \therefore {{U}_{S}}=\frac{{\left( {\sigma _{1}^{2}+\sigma _{2}^{2}+\sigma _{3}^{2}} \right)}}{{2E}}-\frac{{\nu \left( {{{\sigma }_{1}}{{\sigma }_{2}}+{{\sigma }_{2}}{{\sigma }_{3}}+{{\sigma }_{1}}{{\sigma }_{3}}} \right)}}{E}-\frac{{\left( {1-2\nu } \right){{{\left( {{{\sigma }_{1}}+{{\sigma }_{2}}+{{\sigma }_{3}}} \right)}}^{2}}}}{{6E}}$

$\displaystyle \therefore {{U}_{S}}=\frac{{\left( {1+\nu } \right)}}{{6E}}\left[ {{{{\left( {{{\sigma }_{1}}-{{\sigma }_{2}}} \right)}}^{2}}+{{{\left( {{{\sigma }_{2}}-{{\sigma }_{3}}} \right)}}^{2}}+{{{\left( {{{\sigma }_{1}}-{{\sigma }_{3}}} \right)}}^{2}}} \right]\,\,\,\,\,\mathbf{(17)}$

The value of strain energy U_S at the tensile yield point is found by substituting $\displaystyle {{\sigma }_{1}}$ = Y, $\displaystyle {{\sigma }_{2}}$ = $\displaystyle {{\sigma }_{3}}$ = 0 in the foregoing equation,

$\displaystyle {{U}_{S}}=\frac{{\left( {1+\nu } \right)}}{{6E}}\left[ {{{{\left( {Y-0} \right)}}^{2}}+{{{\left( {0-0} \right)}}^{2}}+{{{\left( {Y-0} \right)}}^{2}}} \right]$

$\displaystyle \therefore {{U}_{S}}=\frac{{\left( {1+\nu } \right){{Y}^{2}}}}{{3E}}\,\,\,\,\,\left( {\mathbf{18}} \right)$

Equating (17) and (18) gives

$\displaystyle {{\left( {{{\sigma }_{1}}-{{\sigma }_{2}}} \right)}^{2}}+{{\left( {{{\sigma }_{2}}-{{\sigma }_{3}}} \right)}^{2}}+{{\left( {{{\sigma }_{1}}-{{\sigma }_{3}}} \right)}^{2}}=2{{Y}^{2}}\,\,\,\,\,\left( {\mathbf{19}} \right)$

which is the principal stress form of the von Mises criterion. This equation incorporates, albeit implicitly, some of the assumptions of the von Mises criterion, such as material isotropy and absence of the Bauschinger effect. Specifically, isotropy is implied by the symmetry of the expression with respect to the stress components, while the Bauschinger effect is neglected because only squares of the stress differences are involved (Chakrabarty, 2006).

4. Plane stress yield loci

In several situations of engineering interest, one of the principal stresses may be assumed to vanish, so that the yield criterion can be represented by a single closed curve in the plane formed by the two remaining principal stresses. In Tresca’s yield criterion, the magnitude of the numerically greater of the two principal stresses is equal to Y when these stresses are of the same sign, while the principal stress difference is of magnitude Y when the stresses have opposite signs. Assuming $\displaystyle {{\sigma }_{3}}$ = 0, the Tresca yield locus in the ( $\displaystyle {{\sigma }_{1}}$ , $\displaystyle {{\sigma }_{2}}$ ) plane is represented by a hexagon defined by the straight lines

$\displaystyle {{\sigma }_{1}}=\pm Y\,\,\,\,\,;\,\,\,\,\,{{\sigma }_{2}}=\pm Y\,\,\,\,\,;\,\,\,\,\,{{\sigma }_{1}}-{{\sigma }_{2}}=\pm Y\,\,\,\,\,\mathbf{(20)}$

When $\displaystyle {{\sigma }_{3}}$ = 0, the von Mises criterion, expressed in terms of the principal stresses, reduces to

$\displaystyle \sigma _{1}^{2}-{{\sigma }_{1}}{{\sigma }_{2}}+\sigma _{2}^{2}={{Y}^{2}}\,\,\,\,\,\left( {\mathbf{21}} \right)$

which is the equation of an ellipse whose major and minor axes are inclined at an angle of 45^o with the $\displaystyle {{\sigma }_{1}}$ and $\displaystyle {{\sigma }_{2}}$ axes (Figure 3). The Mises ellipse circumscribes the Tresca hexagon for a given uniaxial yield stress Y.

Figure 3. Tresca hexagon and von Mises ellipse.

5. Comparison between Tresca and von Mises yield criteria

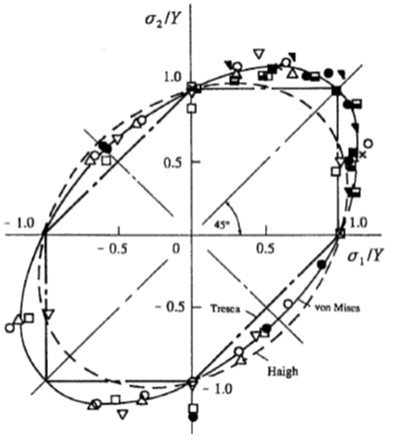
Principal, biaxial stress state. In order to reduce experimental complications, yield loci are routinely obtained via the simplest two-dimensional stress states. A principal, biaxial stress state may be achieved in the wall of a thin-walled tube when it is subjected to combined internal pressure and axial load. The radial strees may be neglected provided the diameter-to-thickness ratio of the tube is high enough. Rees (2006) compiled several such yield point experiments in metals and plotted them as shown in Figure 4. The figure is based on stresses normalized with respect to yield stress Y; the figure includes the Tresca hexagon, the von Mises ellipse, and the Haigh total energy yield criterion. (Please ignore the latter for the present discussion.) The data points representing experimental results are closer to the ellipse than to the hexagon, furnishing evidence that the von Mises yield criterion may hold for initially isotropic, ductile, polycrystalline materials such as several varieties of carbon steel. Further, since most data points lie outside the hexagon, the Tresca criterion may be deemed conservative.

Figure 4. Empirical results for failure of ductile materials in the $\displaystyle {{\sigma }_{1}}{{\sigma }_{2}}$ principal stress plane. From Rees (2006).

Biaxial stress in the $\displaystyle \sigma \tau$ plane. Instead of relying on principal stresses, several workers have reported data on the basis of normal ( $\displaystyle \sigma$ ) and shear ( $\displaystyle \tau$ ) stresses at yield. The experiments used to acquire such data are most often conducted with thin-walled tubes subjected to torsion, combined with either a circumferential tension or an axial tension/compression. Results compiled by Rees (2006) for this approach are plotted in Figure 5. The data reinforce the abovementioned trends that the von Mises locus seems to offer an excellent fit for initially isotropic polycrystalline materials, while the Tresca locus appears to be a conservative tool for assessment of yield behavior.

Figure 5. Empirical results for failure of ductile materials in the $\displaystyle \sigma \tau$ principal stress plane. From Rees (2006).

Reconciling the yield criteria. It is customary to make the two failure criteria agree with each other in uniaxial tension or compression, so that the Mises circle passes through the corners of the Tresca hexagon. The two criteria then have the same value of Y, but the values of shear yield stress will differ considerably. As stated, for most ductile metals the von Mises model defines the yield limit more accurately than does the Tresca model (Chakrabarty, 2006). If the Tresca model is adopted for convenience or simplicity, accuracy can be improved by replacing 2Y in the Tresca relationship ( $\displaystyle {{\sigma }_{1}}$ – $\displaystyle {{\sigma }_{3}}$ ) = 2Y by mY, where m is an empirically assigned number lying between 1.0 and 1.155.

References

Chakrabarty, J. (2006). Theory of Plasticity. 3rd edition. Butterworth-Heinemann.
Han, W. and Reddy, B.D. (2013). Plasticity. 2nd edition. Springer.
Rees, D.W.A. (2006). Basic Engineering Plasticity. Butterworth-Heinemann.
Shames, I.H. and Cozzarelli, F.A. (1997). Elastic and Inelastic Stress Analysis. CRC Press.

Plasticity: Tresca and von Mises Yield Criteria

Subscribe to our Mailing List!

Featured Posts

A Primer on NAND Flash Memories

Solidification Time and Chvorinov’s Rule

Step-Growth Polymerization, the Carothers Equation, and the Flory-Schulz Distribution

More Articles

Shock Wave-Boundary Layer Interaction: Upstream and Downstream Mechanisms

A Quick Introduction to Convective Mass Transfer Correlations

Fields of Study

More

© 2024 Montogue Quiz

Subscribe to
our Mailing List!

Subscribe to our Mailing List!

Subscribe to receive our latest materials in your inbox.

Homework Help

© 2024 Montogue Quiz

Subscribe to our Mailing List!