Bioreactors and Batch Enzyme Conversion

1. Time for batch enzyme conversion

Most commercial bioreactors are mixed vessels operated in batch. The classic mixed reactor is the stirred tank; however, mixed reactors can also be of bubble column, airlift, or other configuration as long as the concentrations of substrate, product, and catalyst inside the vessel are uniform. The cost of running a batch reactor depends on the time taken to achieve the desired product concentration or level of substrate conversion; operating costs are reduced if the reaction is completed quickly. It is therefore useful to be able to predict the time required for batch reactions.

Assuming the Michaelis-Menten model applies, the equation that governs the kinetics of a batch enzyme reactor is

$\displaystyle \frac{{ds}}{{dt}}=-\frac{{{{v}_{{\max }}}s}}{{{{K}_{m}}+s}}$

Here, s is the substrate concentration, $\displaystyle {{v}_{{\max }}}$ is the maximum rate of enzyme reaction, and $\displaystyle {{K}_{m}}$ is the Michaelis constant. Integration of this expression yields an expression for the batch reaction time; we first separate variables:

$\displaystyle -\int_{\,}^{\,}{{dt}}=\int_{\,}^{\,}{{\frac{{{{K}_{m}}+s}}{{{{v}_{{\max }}}s}}ds}}$

Then, integrating with the initial condition $\displaystyle s$ = $\displaystyle {{s}_{0}}$ at t = 0 gives

$\displaystyle {{t}_{b}}=\frac{{{{K}_{m}}}}{{{{v}_{{\max }}}}}\ln \left( {\frac{{{{s}_{0}}}}{{{{s}_{f}}}}} \right)+\frac{{{{s}_{0}}-{{s}_{f}}}}{{{{v}_{{\max }}}}}$

where $\displaystyle {{t}_{b}}$ is the batch reaction time required to reduce the substrate concentration from $\displaystyle {{s}_{0}}$ to $\displaystyle {{s}_{f}}$ . The batch reaction time required to produce a certain concentration of product can be determined with the relation above and stoichiometric relationships.

2. Batch reaction with enzyme deactivation

Enzymes are subject to deactivation. Accordingly, the concentration of active enzyme in the reactor, and therefore the value of $\displaystyle {{v}_{{\max }}}$ , may change during the reaction. When deactivation is significant, the variation of $\displaystyle {{v}_{{\max }}}$ with time can be expressed as

$\displaystyle v=-{{v}_{{\max ,0}}}\exp \left( {-{{k}_{d}}t} \right)$

where $\displaystyle {{v}_{{\max ,0}}}$ is the value of $\displaystyle {{v}_{{\max }}}$ before deactivation occurs and $\displaystyle {{k}_{d}}$ is the first-order deactivation rate constant. Inserting this result in the batch reaction time equation brings to

$\displaystyle \frac{{ds}}{{dt}}=\frac{{-{{v}_{{\max ,0}}}{{e}^{{-{{k}_{d}}t}}}s}}{{{{K}_{m}}+s}}$

Separating variables and integrating, we get

$\displaystyle -\int_{\,}^{\,}{{{{e}^{{-{{k}_{d}}t}}}}}dt=\int_{\,}^{\,}{{\frac{{{{K}_{m}}+s}}{{{{v}_{{\max ,0}}}s}}}}$

$\displaystyle {{t}_{b}}=-\frac{1}{{{{k}_{d}}}}\ln \left\{ {1-{{k}_{d}}\left[ {\frac{{{{K}_{m}}}}{{{{v}_{{\max ,0}}}}}\ln \left( {\frac{{{{s}_{0}}}}{{{{s}_{f}}}}} \right)+\frac{{{{s}_{0}}-{{s}_{f}}}}{{{{v}_{{\max ,0}}}}}} \right]} \right\}$

Having introduced the pertaining equations for batch enzyme reaction kinetics, we proceed to two practical examples. The first, modified from Doran’s Bioprocess Engineering Principles, is a straightforward application of the relations developed heretofore; the second, taken from the problems section of the same textbook, is a simple economic analysis of enzyme reaction kinetics.

Example 1

An enzyme is used to produce a compound used in the manufacture of sunscreen lotion. $\displaystyle {{v}_{{\max }}}$ for the enzyme is 4.0 mmol/m³-s; the Michaelis constant is 9.6 mM. The initial concentration of substrate is 15 mM.

A) Plot the time required for batch reaction as a function of substrate conversion.

B) Assume the enzyme deactivates with a half-life of 3.7 hours. In this case, compute the batch reaction time required to achieve 90% substrate conversion.

As a first step, we convert the units of $\displaystyle {{v}_{{\max }}}$ to mM/h,

$\displaystyle {{v}_{{\max }}}=4.0\,\,\frac{{\text{mmol}}}{{{{\text{m}}^{3}}\cdot \text{s}}}\times \frac{{3600}}{1}\frac{\text{s}}{\text{h}}\times \frac{1}{{1000}}\frac{{{{\text{m}}^{3}}}}{\text{L}}=14.4\,\,{{\text{mM}}}/{\text{h}}\;$

Substituting this and other data in the batch reaction time equation, we have

$\displaystyle {{t}_{b}}=\frac{{9.6}}{{14.4}}\ln \left( {\frac{{15}}{{{{s}_{f}}}}} \right)+\frac{{15-{{s}_{f}}}}{{14.4}}$

The values of $\displaystyle {{t}_{b}}$ for various values of substrate conversion and $\displaystyle {{s}_{f}}$ are tabulated below.

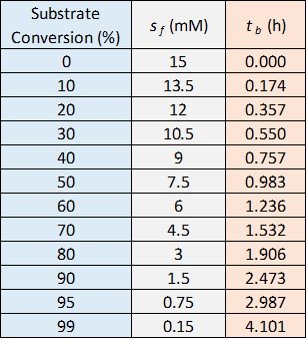
The graph we are looking for is a plot of batch reaction time, the red column, versus substrate conversion, the blue column. The plot in question is shown below.

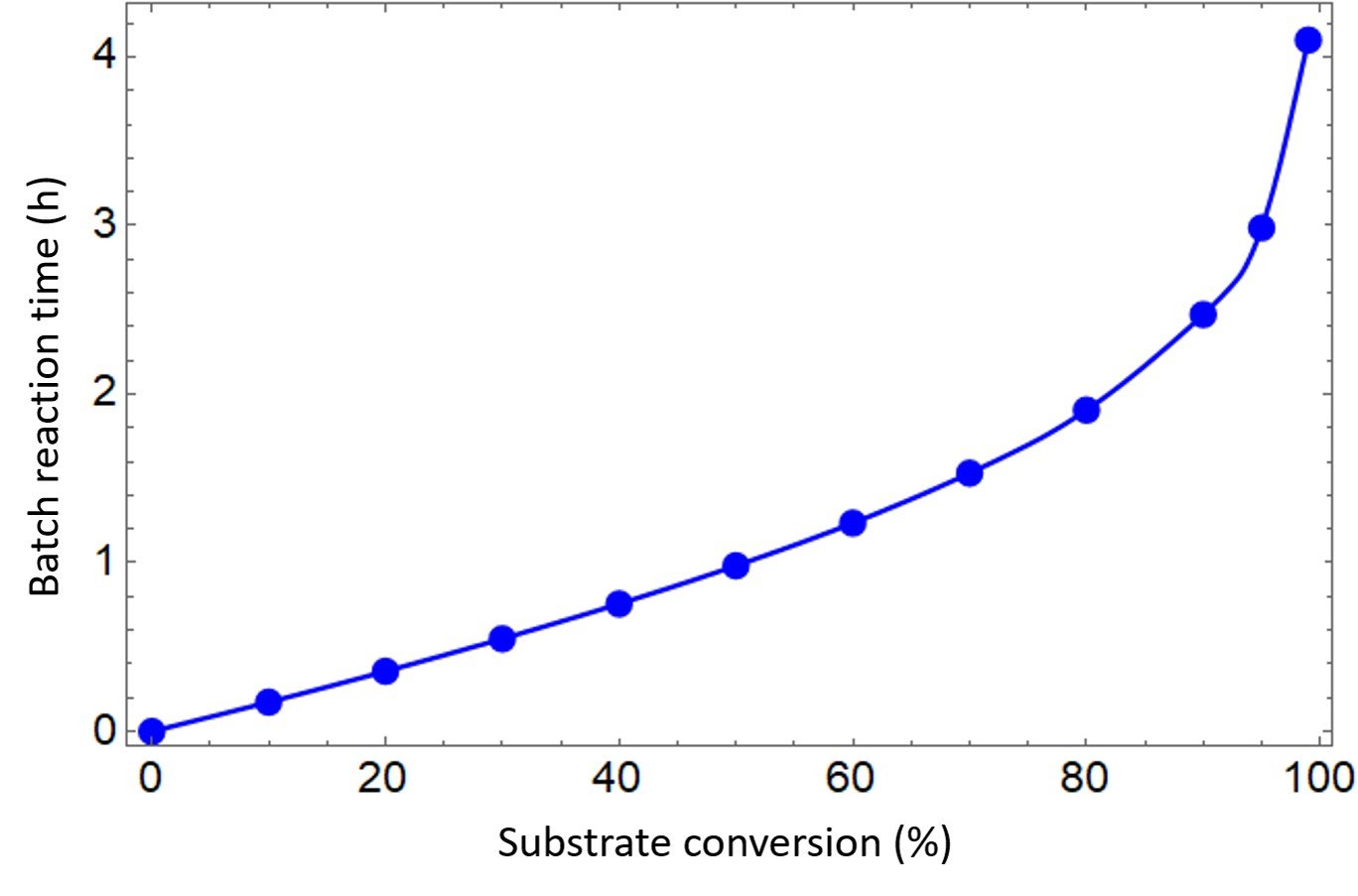
The table and graph indicate that achieving 50% conversion requires about one hour. It also shows that attaining 90% conversion would require about two and a half hours, while 99% conversion takes about four hours.

To answer part B, we must first compute the deactivation rate constant $\displaystyle {{k}_{d}}$ , namely

$\displaystyle {{k}_{d}}=\frac{{\ln 2}}{{{{t}_{{{1}/{2}\;}}}}}=\frac{{0.693}}{{3.7}}=0.187\,\,\text{h}{{\text{r}}^{{-1}}}$

The batch reaction time for 90% conversion is then

$\displaystyle {{t}_{b}}=-\frac{1}{{0.187}}\ln \left\{ {1-0.187\times \left[ {\frac{{9.6}}{{14.4}}\ln \left( {\frac{{15}}{{1.5}}} \right)+\frac{{15-1.5}}{{14.4}}} \right]} \right\}=3.32\,\,\text{h}\leftarrow$

For the enzyme with no deactivation, the time required to achieve the conversion level desired is 2.47 h. Comparing this with the result above, we see that the batch reaction time for the deactivated enzyme is about 34% higher.

Example 2

An enzyme is used to convert substrate to commercial product in a 1500-liter batch reactor. $\displaystyle {{v}_{{\max }}}$ for the enzyme is 1.0 g/L/h; $\displaystyle {{K}_{m}}$ is 1.75 g/L. The substrate concentration at the start of the reaction is 3.2 g/L. According to the reaction stoichiometry, conversion of 1 g of substrate produces 1.2 g of product. The cost of operating the reactor including labor, maintenance, energy and other utilities is estimated at $4500 per day. The cost of recovering the product depends on the substrate conversion achieved and the resulting concentration of product in the final reaction mixture. For conversions between 70 and 100%, the cost of downstream processing can be approximated using the equation

$\displaystyle C=150-0.32X$

where C is the cost in $ per kg of product treated and X is the percentage substrate conversion. Product losses during processing are negligible. The market price for the product is $780/kg. Currently, the enzyme reactor is operated with 75% enzyme conversion; however, it is proposed to increase this to 90%. Estimate the effect that this will have on the economics of the process.

For 75% conversion, $\displaystyle {{s}_{f}}$ = 0.25 $\displaystyle {{s}_{0}}$ . The batch reaction time is calculated as

$\displaystyle {{t}_{b}}=\frac{{{{K}_{m}}}}{{{{v}_{{\max }}}}}\ln \left( {\frac{{{{s}_{0}}}}{{{{s}_{f}}}}} \right)+\frac{{{{s}_{0}}-{{s}_{f}}}}{{{{v}_{{\max }}}}}$

$\displaystyle {{t}_{b}}=\frac{{1.75}}{{1.0}}\ln \left( {\frac{{3.2}}{{0.25\times 3.2}}} \right)+\frac{{3.2-0.25\times 3.2}}{{1.0}}=4.83\,\,\text{h}$

The operating cost is therefore

$\displaystyle \text{Operating cost}=4.83\,\,\text{h}\times \frac{1}{{24}}\,\frac{\text{h}}{{\text{day}}}\times \frac{{\$4500}}{{\text{day}}}=\$906$

The cost of downstream processing per kg of product is

$\displaystyle C=150-0.32\times 75=\$126\,\,\text{k}{{\text{g}}^{{-1}}}$

The mass of product formed is determined from the mass of substrate consumed, which is equal to the change in substrate concentration multiplied by the reactor volume V,

$\displaystyle \text{Mass of substrate consumed}=\left( {{{s}_{0}}-{{s}_{f}}} \right)V=\left( {3.2-0.25\times 3.2} \right)\times 1500=3600\,\,\text{g}$

As 1.2 g product are formed per g of substrate consumed,

$\displaystyle \text{Mass of product formed}=1.2\times 3600=4.32\,\,\text{kg}$

The downstream processing cost follows as

$\displaystyle \text{Downstream processing cost}=\$126\,\text{k}{{\text{g}}^{{-1}}}\times 4.32\,\text{kg}=\$544$

The revenue from sale of the product is

$\displaystyle \text{Revenue}=\$780\,\text{k}{{\text{g}}^{{-1}}}\times 4.32\,\text{kg}=\$3370$

Therefore, the cost benefit at 75% substrate conversion is

$\displaystyle \begin{array}{c}\text{Cost benefit}=\text{Revenue}-\text{Operating cost}-\text{Downstream processing cost}\\\\\text{Cost benefit}=\$3370-\$906-\$544\\\\\text{Cost benefit}=\$1920\end{array}$

We now carry out calculations for 90% conversion. The batch reaction time for $\displaystyle {{s}_{f}}$ = 0.10 $\displaystyle {{s}_{0}}$ is

$\displaystyle {{t}_{b}}=\frac{{1.75}}{{1.0}}\ln \left( {\frac{{3.2}}{{0.1\times 3.2}}} \right)+\frac{{3.2-0.1\times 3.2}}{{1.0}}=6.91\,\text{h}$

At 90% conversion, the operating cost is increased due to the longer reaction time,

$\displaystyle \text{Operating cost}=6.91\ \text{h}\times \frac{1}{{24}}\,\frac{{\text{day}}}{\text{h}}\times \frac{{\$4500}}{{\text{day}}}=\$1300$

The cost of downstream processing per kg of product is

$\displaystyle C=150-0.32\times 90=\$121\,\,\text{k}{{\text{g}}^{{-1}}}$

The mass of substrate consumed is given by

$\displaystyle \text{Mass of substrate consumed}=\left( {{{s}_{0}}-{{s}_{f}}} \right)V=\left( {3.2-0.1\times 3.2} \right)\times 1500=4320\,\,\text{g}$

and the mass of product is

$\displaystyle \text{Mass of product formed}=1.2\times 4320=5.18\,\,\text{kg}$

The corresponding downstream processing cost is

$\displaystyle \text{Downstream processing cost}=\$121\,\text{k}{{\text{g}}^{{-1}}}\times 5.18\,\text{kg}=\$627$

The sales revenue is

$\displaystyle \text{Revenue}=\$780\,\text{k}{{\text{g}}^{{-1}}}\times 5.18\,\text{kg}=\$4040$

Finally, the cost benefit at 90% conversion is calculated to be

$\displaystyle \begin{array}{c}\text{Cost benefit}=\text{Revenue}-\text{Operating cost}-\text{Downstream processing cost}\\\\\text{Cost benefit}=\$4040-\$1300-\$627\\\\\text{Cost benefit}=\$2113\end{array}$

The gain per batch from increasing the conversion as proposed is $2113 – $1920 = $193. This represents a 10% increase in cost benefit, and hence may be worth pursuing.

Go further

Montogue offers two free sets of solved problems on bioprocess engineering; part 1 can be found here and part 2 here. Those looking for a review of general microbiology may also enjoy our free quiz on this subject.

Reference

• DORAN, P. (2013). Bioprocess Engineering Principles. 2nd edition. London: Academic Press.

Bioreactors and Batch Enzyme Conversion

Subscribe to our Mailing List!

Featured Posts

A Primer on NAND Flash Memories

Solidification Time and Chvorinov’s Rule

Step-Growth Polymerization, the Carothers Equation, and the Flory-Schulz Distribution

More Articles

Tokamaks and the Grad-Shafranov Equation

A Quick Introduction to Convective Mass Transfer Correlations

Fields of Study

More

© 2024 Montogue Quiz

Subscribe to
our Mailing List!

Subscribe to our Mailing List!

Subscribe to receive our latest materials in your inbox.

Homework Help

© 2024 Montogue Quiz

Subscribe to our Mailing List!