Chemical Equilibrium Thermodynamics and Extent of Reaction: Step by Step

In this article, we investigate single-reaction gas-phase equilibria; specifically, we show how one can easily determine the equilibrium composition with knowledge of the equilibrium constant K. As the student surely knows, any typical chemical reaction can be represented by the general notation

$\displaystyle \left| {{{v}_{1}}} \right|{{A}_{1}}\,+\left| {{{v}_{2}}} \right|{{A}_{2}}+\left( {...} \right)\to \left| {{{v}_{3}}} \right|{{A}_{3}}+\left| {{{v}_{4}}} \right|{{A}_{4}}+\left( {...} \right)$

where $\displaystyle A$ is a placeholder for the formula of a chemical species and $\displaystyle {{v}_{i}}$ is a stoichiometric coefficient. The symbol $\displaystyle {{v}_{i}}$ itself is a stoichiometric number, and by the sign convention adopted in most textbooks, it is associated with a positive sign (+) for a product or a negative sign (-) for a reactant. For instance, in the reaction studied in Example 1 below,

$\displaystyle 4\text{HC}{{\text{l}}_{{\left( \text{g} \right)}}}+{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}\to 2{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{g} \right)}}}+2\text{C}{{\text{l}}_{{\text{2}\left( \text{g} \right)}}}$

the stoichiometric numbers are

$\displaystyle {{v}_{{HCl}}}=-4\,\,\,;\,\,\,{{v}_{{{{O}_{2}}}}}=-1\,\,\,;\,\,\,{{v}_{{{{\text{H}}_{\text{2}}}\text{O}}}}=2\,\,\,;\,\,{{v}_{{\text{C}{{\text{l}}_{2}}}}}=2$

The number of moles $\displaystyle {{n}_{i}}$ of a given reactant/product is related to the stoichiometric number by an expression of the form

$\displaystyle d{{n}_{i}}={{v}_{i}}d\varepsilon$

where we have introduced a variable $\displaystyle \varepsilon$ , known as the reaction coordinate, which describes the extent or degree to which a reaction has taken place. Integrating the relation above gives

$\displaystyle {{n}_{i}}={{n}_{{i,0}}}+{{v}_{i}}\varepsilon$

Summation over all species yields

$\displaystyle n=\sum\limits_{i}{{{{n}_{i}}}}=\sum\limits_{i}{{{{n}_{{i,0}}}}}+\varepsilon \sum\limits_{i}{{{{v}_{i}}}}$

$\displaystyle \therefore n={{n}_{0}}+v\varepsilon$

The mole fractions $\displaystyle {{y}_{i}}$ of the species present are expressed as

$\displaystyle {{y}_{i}}=\frac{{{{n}_{i}}}}{n}=\frac{{{{n}_{{i,0}}}+{{v}_{i}}\varepsilon }}{{{{n}_{0}}+v\varepsilon }}\,\,\,(\text{I})$

In a gas-phase reaction, the molar fractions, the system presure, and the so-called equilibrium constant are related by an expression of the form

$\displaystyle {{\prod\limits_{i}{{\left( {{{y}_{i}}{{{\hat{\phi }}}_{i}}} \right)}}}^{{{{v}_{i}}}}}={{\left( {\frac{P}{{{{P}^{o}}}}} \right)}^{{-v}}}K$

Here, $\displaystyle {{y}_{i}}$ is the molar fraction of component i, $\displaystyle {{\phi }_{i}}$ is the fugacity coefficient of component i, $\displaystyle {{v}_{i}}$ is the stoichiometric coefficient of species i, $\displaystyle P$ is pressure, $\displaystyle {{P}_{0}}$ is the reference pressure (usually taken as 1 bar), $\displaystyle v$ is the reaction stoichiometric number, and $\displaystyle K$ is the equilibrium constant. For ideal gases, the fugacity coefficient equals unity and the equation simplifies to

$\displaystyle \prod\limits_{i}{{{{{\left( {{{y}_{i}}} \right)}}^{{{{v}_{i}}}}}}}={{\left( {\frac{P}{{{{P}_{0}}}}} \right)}^{{-v}}}K\,\,\,(\text{II})$

In words, the scary product on the left-hand side simply means that we should multiply in series the molar fractions of each component i, taken to a power equal to its stoichiometric coefficient. Consider, for instance, the simple equilibrium

$\displaystyle {{\text{N}}_{\text{2}}}{{\text{O}}_{{\text{4}\left( \text{g} \right)}}}\to 2\text{N}{{\text{O}}_{{2\left( \text{g} \right)}}}$

Here, $\displaystyle {{\text{N}}_{\text{2}}}{{\text{O}}_{\text{4}}}$ has a stoichiometric number $\displaystyle v$ = -1 and $\displaystyle \text{N}{{\text{O}}_{\text{2}}}$ has $\displaystyle v$ = 1. Denoting by $\displaystyle {{y}_{{{{N}_{2}}{{O}_{4}}}}}$ the molar fraction of dinitrogen tetroxide and by $\displaystyle {{y}_{{N{{O}_{2}}}}}$ the molar fraction of nitrogen dioxide, we write

$\displaystyle \prod\limits_{i}^{\,}{{{{{\left( {{{y}_{i}}} \right)}}^{v}}}}={{\left( {{{y}_{{{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{4}}}}}}} \right)}^{{-1}}}\times {{\left( {{{y}_{{N{{O}_{2}}}}}} \right)}^{2}}=\frac{{y_{{N{{O}_{2}}}}^{2}}}{{{{y}_{{{{N}_{2}}{{O}_{4}}}}}}}$

The molar fractions can be shown to be

$\displaystyle {{y}_{{{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{4}}}}}}=\frac{{1-\varepsilon }}{{1+\varepsilon }}\,\,\,;\,\,\,{{y}_{{N{{O}_{2}}}}}=\frac{{2\varepsilon }}{{1+\varepsilon }}$

so that

$\displaystyle \frac{{{{{\left( {2\varepsilon } \right)}}^{2}}}}{{\left( {1-\varepsilon } \right)\left( {1+\varepsilon } \right)}}={{\left( {\frac{P}{{{{P}_{0}}}}} \right)}^{{-1}}}K$

Clearly, determining the extent of reaction $\displaystyle \varepsilon$ becomes a matter of evaluating the equilibrium constant K. This quantity is expressed in terms of the reaction change in Gibbs free energy as

$\displaystyle \Delta {{G}^{\text{o}}}=-RT\ln K$

The value of $\displaystyle \Delta {{G}^{\text{o}}}$ at the reaction temperature T can be estimated with the relation

$\displaystyle \frac{{\Delta {{G}^{\text{o}}}}}{{RT}}=\frac{{\Delta G_{0}^{\text{o}}-\Delta H_{0}^{\text{o}}}}{{R{{T}_{0}}}}+\frac{{\Delta H_{0}^{\text{o}}}}{{RT}}+\frac{1}{T}\int_{{{{T}_{0}}}}^{T}{{\frac{{\Delta C_{p}^{\text{o}}}}{R}dT-\int_{{{{T}_{0}}}}^{T}{{\frac{{\Delta C_{p}^{\text{o}}}}{R}\frac{{dT}}{T}}}}}\,\,\,(\text{III})$

Here, subscript “0” denotes a quantity expressed at the reference temperature $\displaystyle {{T}_{0}}$ , usually 298 K. Given the heats of formation $\displaystyle \Delta H_{f}^{\text{o}}$ and the change in Gibbs free energies of formation $\displaystyle \Delta G_{f}^{\text{o}}$ , the values of $\displaystyle \Delta H_{{298}}^{\text{o}}$ and $\displaystyle \Delta G_{{298}}^{\text{o}}$ can be easily determined. The heat capacity integrals on the right-hand side can be computed with the general expressions

$\displaystyle \int_{{{{T}_{0}}}}^{T}{{\frac{{\Delta C_{p}^{\text{o}}}}{R}dT}}=\Delta A{{T}_{0}}\left( {\tau -1} \right)+\frac{{\Delta B}}{2}T_{0}^{2}\left( {{{\tau }^{2}}-1} \right)+\frac{{\Delta C}}{3}T_{0}^{3}\left( {{{\tau }^{3}}-1} \right)+\frac{{\Delta D}}{{{{T}_{0}}}}\left( {\frac{{\tau -1}}{\tau }} \right)$

$\displaystyle \int_{{{{T}_{0}}}}^{T}{{\frac{{\Delta C_{p}^{\text{o}}}}{R}\frac{{dT}}{T}}}=\Delta A\ln \tau +\left[ {\Delta B{{T}_{0}}+\left( {\Delta CT_{0}^{2}+\frac{{\Delta D}}{{{{\tau }^{2}}T_{0}^{2}}}} \right)\left( {\frac{{\tau +1}}{2}} \right)} \right]\left( {\tau -1} \right)$

in which $\displaystyle \tau$ = $\displaystyle T$ / $\displaystyle {{T}_{0}}$ is the temperature ratio and the $\displaystyle \Delta$ ‘s are, by definition,

$\displaystyle \Delta A=\sum\limits_{i}{{{{v}_{i}}{{A}_{i}}}}\,\,\,;\,\,\,\Delta B=\sum\limits_{i}{{{{v}_{i}}{{B}_{i}}}}\,\,\,;\,\,\,\Delta C=\sum\limits_{i}{{{{v}_{i}}{{C}_{i}}}}\,\,\,;\,\,\,\Delta D=\sum\limits_{i}{{{{v}_{i}}{{D}_{i}}}}$

Having evaluated all terms on the right-hand side of equation (III), the reaction change in Gibbs free energy $\displaystyle \Delta G$ and thence the equilibrium constant $\displaystyle K$ can be established. Lastly, the extent of reaction and thence the molar fractions can be determined with equation (II). The steps are summarized below.

Step 1. With the initial number of moles and stoichiometric coefficients, determine expressions for the molar fractions using equation (I).

Step 2. Substitute the molar fractions into equation (II) to determine an expression that relates the extent of reaction $\displaystyle \varepsilon$ to the equilibrium constant K.

Step 3. Determine the heat of reaction $\displaystyle \Delta H_{{298}}^{\text{o}}$ and the change in Gibbs free energy $\displaystyle \Delta G_{{298}}^{\text{o}}$ at 298 K.

Step 4. Using the temperature ratio $\displaystyle \tau$ and the $\displaystyle \Delta$ coefficients, evaluate the heat capacity integrals.

Step 5. Using the results from steps 3 and 4, determine the right-hand side of equation (III).

Step 6. Knowing that $\displaystyle -\ln K={{\Delta {{G}^{\text{o}}}}}/{{RT}}\;$ , determine the equilibrium constant K.

Step 7. Substituting K in the expression determined in step 2, determine the extent of reaction $\displaystyle \varepsilon$ .

Step 8. Substitute $\displaystyle \varepsilon$ in the expressions derived in step 1 and determine the mole fractions.

We now present two applied examples.

Example 1

The following reaction reaches equilibrium at 500ºC and 2 bar:

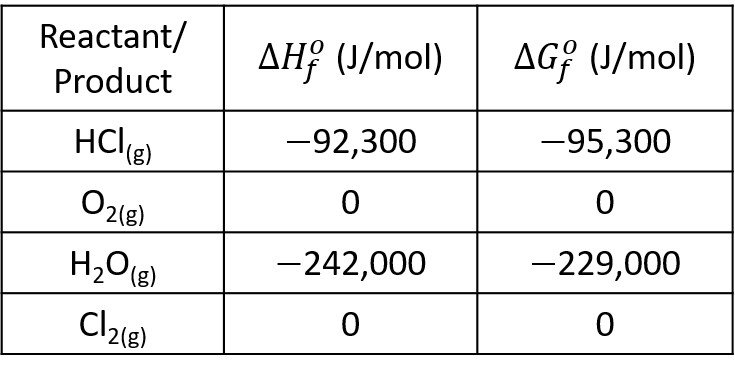
$\displaystyle 4\text{HC}{{\text{l}}_{{\left( \text{g} \right)}}}+{{\text{O}}_{{2\left( \text{g} \right)}}}\to 2{{\text{H}}_{\text{2}}}{{\text{O}}_{{\text{(g)}}}}+2\text{C}{{\text{l}}_{{2\left( \text{g} \right)}}}$

If the system initially contains 5 mol of HCl for each mole of oxygen, what is the composition of the system at equilibrium? Assume ideal gases. Use the following data.

The molar balance is outlined below.

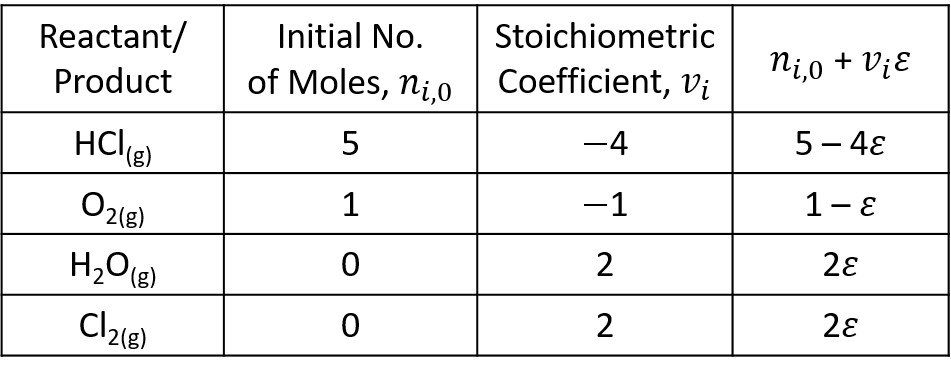
The total No. of moles at the beginning of the reaction is

$\displaystyle {{n}_{0}}=\sum\limits_{i}^{\,}{{{{n}_{{i,0}}}}}=5+1=6$

The product of reaction stoichiometric number and extent of reaction is

$\displaystyle v\varepsilon =\left( {\sum\limits_{i}{{{{v}_{i}}}}} \right)\varepsilon =\left( {-4-1+2+2} \right)\times \varepsilon =-\varepsilon$

The mole fractions of each component are written next.

$\displaystyle y=\frac{{{{n}_{{i,0}}}+{{v}_{i}}\varepsilon }}{{{{n}_{0}}+v\varepsilon }}$

$\displaystyle {{y}_{{\text{HCl}}}}=\frac{{5-4\varepsilon }}{{6-\varepsilon }}$

$\displaystyle {{y}_{{{{\text{O}}_{\text{2}}}}}}=\frac{{1-\varepsilon }}{{6-\varepsilon }}$

$\displaystyle {{y}_{{{{\text{H}}_{\text{2}}}\text{O}}}}=\frac{{2\varepsilon }}{{6-\varepsilon }}$

$\displaystyle {{y}_{{\text{C}{{\text{l}}_{2}}}}}=\frac{{2\varepsilon }}{{6-\varepsilon }}$

The equilibrium constant, pressure, and composition are related by equation (II),

$\displaystyle \frac{{y_{{{{H}_{2}}O}}^{2}\times y_{{C{{l}_{2}}}}^{2}}}{{{{y}_{{{{O}_{2}}}}}\times y_{{\text{HCl}}}^{4}}}={{\left( {\frac{P}{{{{P}_{0}}}}} \right)}^{{-v}}}K$

Substituting the molar fractions, $\displaystyle P$ = 2 bar, $\displaystyle {{P}_{0}}$ = 1 bar, and $\displaystyle v$ = -1 gives

$\displaystyle \frac{{{{{\left( {\frac{{2\varepsilon }}{{6-\varepsilon }}} \right)}}^{2}}\times {{{\left( {\frac{{2\varepsilon }}{{6-\varepsilon }}} \right)}}^{2}}}}{{\left( {\frac{{1-\varepsilon }}{{6-\varepsilon }}} \right)\times {{{\left( {\frac{{5-4\varepsilon }}{{6-\varepsilon }}} \right)}}^{4}}}}={{\left( {\frac{2}{1}} \right)}^{{-\left( {-1} \right)}}}K=2K\,\,\,(\text{IV})$

It remains to compute the equilibrium constant K. In step 3, we calculate the heat of reaction at 298 K,

$\displaystyle \Delta H_{{298}}^{\text{o}}=\left[ {2\Delta H_{{f,298}}^{\text{o}}\left( {{{\text{H}}_{\text{2}}}\text{O}} \right)+2\Delta H_{{f,298}}^{\text{o}}\left( {\text{C}{{\text{l}}_{\text{2}}}} \right)} \right]-\left[ {4\Delta H_{{f,298}}^{\text{o}}\left( {\text{HCl}} \right)+\Delta H_{{f,298}}^{\text{o}}\left( {{{\text{O}}_{\text{2}}}} \right)} \right]$

$\displaystyle \therefore \Delta H_{{298}}^{\text{o}}=\left[ {2\times \left( {-242,000} \right)+2\times 0} \right]-\left[ {4\times \left( {-92,300} \right)+0} \right]=-114,800\,\,\text{J/mol}$

and the change in Gibbs free energy at 298 K,

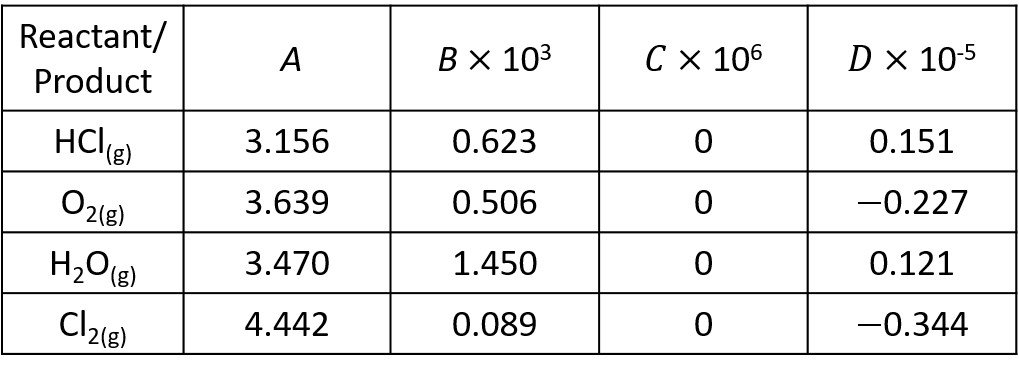
$\displaystyle \Delta G_{{298}}^{\text{o}}=\left[ {2\Delta G_{{f,298}}^{\text{o}}\left( {{{\text{H}}_{\text{2}}}\text{O}} \right)+2\Delta G_{{f,298}}^{\text{o}}\left( {\text{C}{{\text{l}}_{\text{2}}}} \right)} \right]-\left[ {4\Delta G_{{f,298}}^{\text{o}}\left( {\text{HCl}} \right)+\Delta G_{{f,298}}^{\text{o}}\left( {{{\text{O}}_{\text{2}}}} \right)} \right]$

$\displaystyle \therefore \Delta G_{{298}}^{\text{o}}=\left[ {2\times \left( {-229,000} \right)+2\times 0} \right]-\left[ {4\times \left( {-95,300} \right)+0} \right]=-76,800\,\,\text{J/mol}$

Next, we compute the $\displaystyle \,\Delta$ coefficients for use with the heat capacity integrals.

$\displaystyle \,\Delta A=\sum\limits_{i}^{\,}{{{{v}_{i}}{{A}_{i}}}}=2\times 3.470+2\times 4.442-4\times 3.156-1\times 3.639=-0.439$

$\displaystyle \,\Delta B=\sum\limits_{i}^{\,}{{{{v}_{i}}{{B}_{i}}}}=\left( {2\times 1.45+2\times 0.089-4\times 0.623-1\times 0.506} \right)\times {{10}^{{-3}}}=8\times {{10}^{{-5}}}$

$\displaystyle \,\Delta C=\sum\limits_{i}^{\,}{{{{v}_{i}}{{C}_{i}}}}=0$

$\displaystyle \,\Delta D=\sum\limits_{i}^{\,}{{{{v}_{i}}{{D}_{i}}}}=\left[ {2\times 0.121+2\times \left( {-0.344} \right)-4\times 0.151-1\times \left( {-0.227} \right)} \right]\times {{10}^{5}}=-8.23\times {{10}^{4}}$

Now, the temperature ratio is $\displaystyle \tau$ = 773/298 = 2.59. In step 4, we evaluate the enthalpy integral

$\displaystyle \int_{{298}}^{{773}}{{\frac{{\Delta C_{p}^{\text{o}}}}{R}dT}}=\Delta A{{T}_{0}}\left( {\tau -1} \right)+\frac{{\Delta B}}{2}T_{0}^{2}\left( {{{\tau }^{2}}-1} \right)+\frac{{\Delta C}}{3}T_{0}^{3}\left( {{{\tau }^{3}}-1} \right)+\frac{{\Delta D}}{{{{T}_{0}}}}\left( {\frac{{\tau -1}}{\tau }} \right)$

$\displaystyle \int_{{298}}^{{773}}{{\frac{{\Delta C_{p}^{\text{o}}}}{R}dT}}=-0.439\times 298\times \left( {2.59-1} \right)+\frac{{\left( {8\times {{{10}}^{{-5}}}} \right)}}{2}\times {{298}^{2}}\times \left( {{{{2.59}}^{2}}-1} \right)+0-\frac{{\left( {8.23\times {{{10}}^{{-4}}}} \right)}}{{298}}\left( {\frac{{2.59-1}}{{2.59}}} \right)$

$\displaystyle \therefore \int_{{298}}^{{773}}{{\frac{{\Delta C_{p}^{\text{o}}}}{R}dT}}=-357$

and the entropy integral

$\displaystyle \int_{{298}}^{{773}}{{\frac{{\Delta {{C}_{p}}}}{R}\frac{{dT}}{T}}}=\Delta A\ln \tau +\left[ {\Delta B{{T}_{0}}+\left( {\Delta CT_{0}^{2}+\frac{{\Delta D}}{{{{\tau }^{2}}T_{0}^{2}}}} \right)\left( {\frac{{\tau +1}}{2}} \right)} \right]\left( {\tau -1} \right)$

$\displaystyle \therefore \int_{{298}}^{{773}}{{\frac{{\Delta C_{p}^{\text{o}}}}{R}\frac{{dT}}{T}}}=-0.439\times \ln \left( {2.59} \right)+\left[ {\left( {8\times {{{10}}^{{-5}}}} \right)\times 298+\left( {0-\frac{{8.23\times {{{10}}^{4}}}}{{{{{2.59}}^{2}}\times {{{298}}^{2}}}}} \right)\left( {\frac{{2.59+1}}{2}} \right)} \right]\left( {2.59-1} \right)$

$\displaystyle \therefore \int_{{298}}^{{773}}{{\frac{{\Delta C_{p}^{\text{o}}}}{R}\frac{{dT}}{T}}}=-0.774$

We now have all the information necessary to calculate $\displaystyle -\ln K$ . Indeed,

$\displaystyle -\ln K=\frac{{\Delta G_{{298}}^{\text{o}}-\Delta H_{{298}}^{\text{o}}}}{{R{{T}_{0}}}}+\frac{{\Delta H_{{298}}^{\text{o}}}}{{RT}}+\frac{1}{T}\int_{{298}}^{{773}}{{\frac{{\Delta C_{p}^{\text{o}}}}{R}dT}}-\int_{{298}}^{{773}}{{\frac{{\Delta C_{p}^{\text{o}}}}{R}\frac{{dT}}{T}}}$

$\displaystyle \therefore -\ln K=\frac{{-76,800-\left( {-114,800} \right)}}{{8.314\times 298}}-\frac{{114,800}}{{8.314\times 773}}+\frac{1}{{773}}\times \left( {-357} \right)-\left( {-0.774} \right)=-2.21$

Resolving the logarithm,

$\displaystyle \ln K=2.21\to K=9.12$

Substituting in equation (IV) yields

Adjusting the fraction on the left-hand side, we have

$\displaystyle \frac{{16{{\varepsilon }^{4}}\left( {6-\varepsilon } \right)}}{{{{{\left( {5-4\varepsilon } \right)}}^{4}}\left( {1-\varepsilon } \right)}}=18.2$

The equation above is a fifth-degree polynomial in $\displaystyle \varepsilon$ and does not lend itself to elementary methods of solution. One way to go is to apply Mathematica’s Solve command,

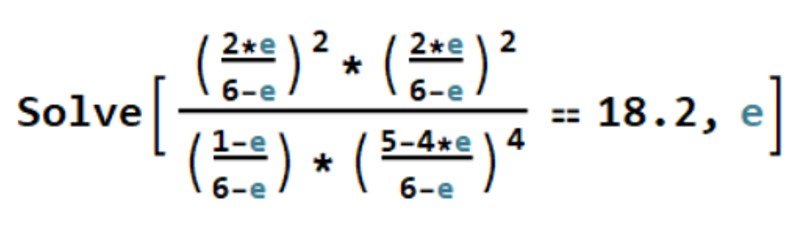
This returns four imaginary solutions and $\displaystyle \varepsilon$ = 0.806, which is a valid result. The extent of reaction has been determined. It remains to compute the molar fractions, namely

$\displaystyle {{y}_{{\text{HCl}}}}=\frac{{5-4\times 0.806}}{{6-0.806}}=0.342$

$\displaystyle {{y}_{{{{O}_{2}}}}}=\frac{{1-0.806}}{{6-0.806}}=0.0374$

$\displaystyle {{y}_{{{{H}_{2}}O}}}=\frac{{2\varepsilon }}{{6-\varepsilon }}=\frac{{2\times 0.806}}{{6-0.806}}=0.310$

$\displaystyle {{y}_{{C{{l}_{2}}}}}={{y}_{{{{H}_{2}}O}}}=0.310$

The sum of molar fractions is such that

$\displaystyle \Sigma y=0.342+0.0374+0.310+0.310=0.9994\approx 1.0$

as it should be. The slight difference is due to roundoff. Our results are tabulated below.

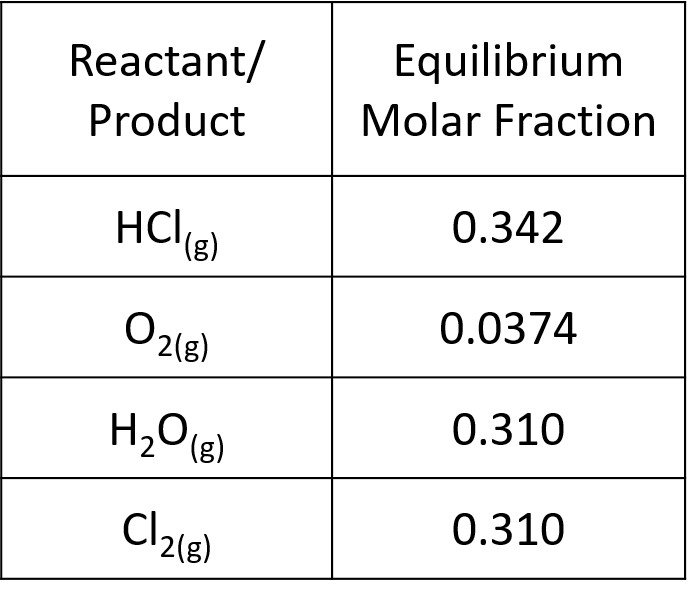
Example 2

Oil refineries frequently have both $\displaystyle {{\text{H}}_{2}}\text{S}$ and $\displaystyle \text{S}{{\text{O}}_{\text{2}}}$ to dispose of. The following reaction suggests a means of getting rid of both at once:

$\displaystyle \text{2}{{\text{H}}_{2}}{{\text{S}}_{{\left( \text{g} \right)}}}+\text{S}{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}\to 3{{\text{S}}_{{\left( \text{s} \right)}}}+2{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{g} \right)}}}$

For reactants in the stoichiometric proportion, estimate the molar fraction of each reactant if the reaction comes to equilibrium at 450ºC and 8 bar. Use the following data.

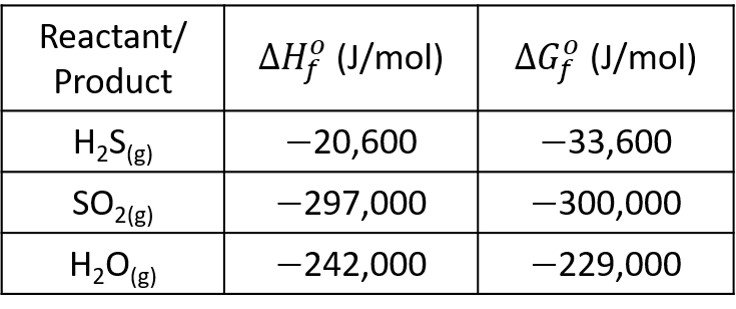
The sulfur exists pure as a solid phase, for which the activity is $\displaystyle f$ / $\displaystyle {{f}_{0}}$ . Since $\displaystyle f$ and $\displaystyle {{f}_{0}}$ are for practical purposes the same, the activity is unit, and it is omitted from the equilibrium equation. Having established this, we turn to the molar balance of the three other species involved in the reaction.

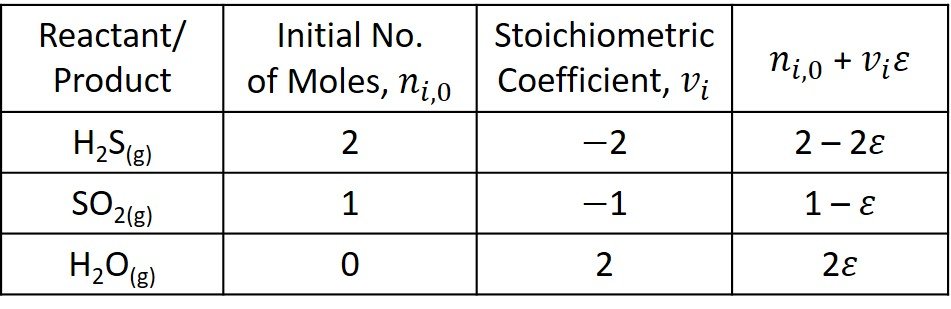
The total No. of moles at the beginning of the reaction is

$\displaystyle {{n}_{0}}=\sum\limits_{i}^{\,}{{{{n}_{{i,0}}}}}=2+1=3$

The product of reaction stoichiometric number and extent of reaction is

$\displaystyle v\varepsilon =\left( {\sum\limits_{i}{{{{v}_{i}}}}} \right)\varepsilon =\left( {-2-1+2} \right)\times \varepsilon =-\varepsilon$

The mole fractions of each component are written next.

$\displaystyle {{y}_{{{{H}_{2}}S}}}=\frac{{2-2\varepsilon }}{{3-\varepsilon }}$

$\displaystyle {{y}_{{S{{O}_{2}}}}}=\frac{{1-\varepsilon }}{{3-\varepsilon }}$

$\displaystyle {{y}_{{{{H}_{2}}O}}}=\frac{{2\varepsilon }}{{3-\varepsilon }}$

The equilibrium constant, pressure, and composition are related by equation (II),

$\displaystyle \frac{{y_{{{{H}_{2}}O}}^{2}}}{{y_{{{{\text{H}}_{2}}S}}^{2}\times {{y}_{{S{{O}_{2}}}}}}}={{\left( {\frac{P}{{{{P}_{0}}}}} \right)}^{{-v}}}K$

Substituting the molar fractions, $\displaystyle P$ = 8 bar, $\displaystyle {{P}_{0}}$ = 1 bar, and $\displaystyle v$ = -1 gives

$\displaystyle \frac{{{{{\left( {\frac{{2\varepsilon }}{{3-\varepsilon }}} \right)}}^{2}}}}{{{{{\left( {\frac{{2-2\varepsilon }}{{3-\varepsilon }}} \right)}}^{2}}\times \left( {\frac{{1-\varepsilon }}{{3-\varepsilon }}} \right)}}={{\left( {\frac{8}{1}} \right)}^{{-\left( {-1} \right)}}}K=8K\,\,\,(\text{V})$

The heat of reaction at 298 K is

$\displaystyle \Delta H_{{298}}^{\text{o}}=\left[ {2\Delta H_{{f,298}}^{\text{o}}\left( {{{\text{H}}_{\text{2}}}\text{O}} \right)} \right]-\left[ {2\Delta H_{{f,298}}^{\text{o}}\left( {{{\text{H}}_{\text{2}}}\text{S}} \right)+\Delta H_{{f,298}}^{\text{o}}\left( {\text{S}{{\text{O}}_{\text{2}}}} \right)} \right]$

$\displaystyle \therefore \Delta H_{{298}}^{\text{o}}=\left[ {2\times \left( {-242,000} \right)} \right]-\left[ {2\times \left( {-20,600} \right)+\left( {-297,000} \right)} \right]=-145,800\,\,\text{J/mol}$

and the change in Gibbs free energy at 298 K is

$\displaystyle \Delta G_{{298}}^{\text{o}}=\left[ {2\Delta G_{{f,298}}^{\text{o}}\left( {{{\text{H}}_{\text{2}}}\text{O}} \right)} \right]-\left[ {2\Delta G_{{f,298}}^{\text{o}}\left( {{{\text{H}}_{\text{2}}}\text{S}} \right)+\Delta G_{{f,298}}^{\text{o}}\left( {\text{S}{{\text{O}}_{\text{2}}}} \right)} \right]$

$\displaystyle \therefore \Delta G_{{298}}^{\text{o}}=\left[ {2\times \left( {-229,000} \right)} \right]-\left[ {2\times \left( {-33,600} \right)+\left( {-300,000} \right)} \right]=-90,800\,\,\text{J/mol}$

Next, we compute the $\displaystyle \,\Delta$ coefficients for use with the heat capacity integrals.

$\displaystyle \Delta A=\sum\limits_{i}{{{{v}_{i}}{{A}_{i}}}}=2\times 3.470+3\times 4.114-2\times 3.931-1\times 5.699=5.72$

$\displaystyle \Delta B=\sum\limits_{i}{{{{v}_{i}}{{B}_{i}}}}=\left[ {2\times 1.490+3\times \left( {-1.728} \right)-2\times 1.450-1\times 0.801} \right]\times {{10}^{{-3}}}=-5.99\times {{10}^{{-3}}}$

$\displaystyle \Delta C=0$

$\displaystyle \Delta D=\left[ {2\times 0.121+3\times \left( {-0.783} \right)-2\times \left( {-0.232} \right)-1\times \left( {-1.015} \right)} \right]\times {{10}^{5}}=-6.28\times {{10}^{4}}$

Now, the temperature ratio is $\displaystyle \tau$ = 723/298 = 2.43. In step 4, we evaluate the enthalpy integral

$\displaystyle \int_{{298}}^{{723}}{{\frac{{\Delta C_{p}^{\text{o}}}}{R}dT}}=5.72\times 298\times \left( {2.43-1} \right)-\frac{{5.99\times {{{10}}^{{-3}}}}}{2}\times {{298}^{2}}\times \left( {{{{2.43}}^{2}}-1} \right)+0-\frac{{6.28\times {{{10}}^{4}}}}{{298}}\times \left( {\frac{{2.43-1}}{{2.43}}} \right)=1010$

and the entropy integral

$\displaystyle \int_{{298}}^{{723}}{{\frac{{\Delta C_{p}^{\text{o}}}}{R}\frac{{dT}}{T}}}=5.72\times \ln \left( {2.43} \right)+\left[ {\left( {-5.99\times {{{10}}^{{-3}}}} \right)\times 298+\left( {0-\frac{{6.28\times {{{10}}^{4}}}}{{2.43\times {{{10}}^{2}}\times {{{298}}^{2}}}}} \right)\times \left( {\frac{{2.43+1}}{2}} \right)} \right]\times \left( {2.43-1} \right)$

$\displaystyle \therefore \int_{{298}}^{{723}}{{\frac{{\Delta C_{p}^{\text{o}}}}{R}\frac{{dT}}{T}}}=2.23$

We can now establish the value of $\displaystyle -\ln K$ ,

$\displaystyle -\ln K=\frac{{-90,800-\left( {-145,800} \right)}}{{8.314\times 298}}-\frac{{145,800}}{{8.314\times 723}}+\frac{1}{{723}}\times 1010-2.23$

$\displaystyle \therefore -\ln K=-2.89$

Resolving the logarithm,

$\displaystyle K={{e}^{{2.89}}}=18.0$

Substituting in equation (V) yields

As before, we can solve the ensuing equation with Mathematica’s Solve command,

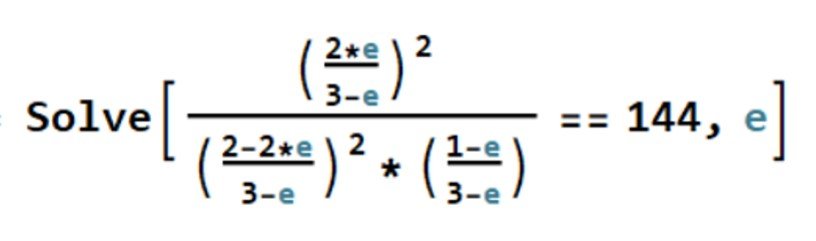
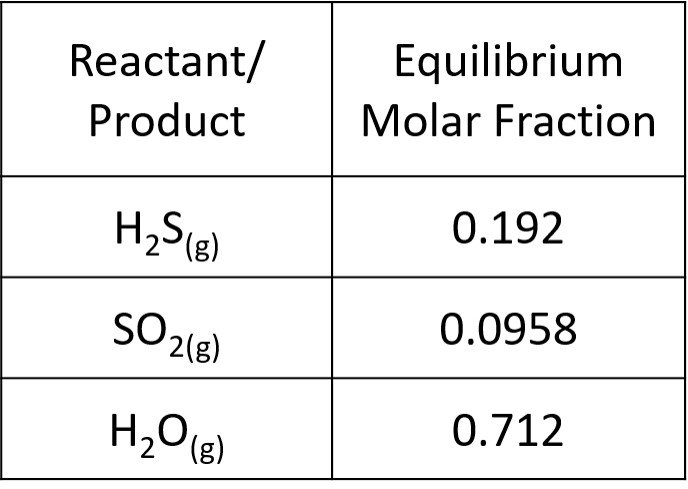
This returns two imaginary solutions and $\displaystyle \varepsilon$ = 0.788, which is a feasible result. The extent of reaction has been established. Lastly, we can determine the equilibrium mole fractions,

$\displaystyle {{y}_{{{{H}_{2}}S}}}=\frac{{2-2\times 0.788}}{{3-0.788}}=0.192$

$\displaystyle {{y}_{{S{{O}_{2}}}}}=\frac{{1-0.788}}{{3-0.788}}=0.0958$

$\displaystyle {{y}_{{{{H}_{2}}O}}}=\frac{{2\times 0.788}}{{3-0.788}}=0.712$

The sum of molar fractions is

$\displaystyle \Sigma y=0.192+0.0958+0.712=0.9998\approx 1.0$

as one would expect. The results are summarized below.

Reference

• SMITH, J., VAN NESS, H. and ABBOTT, M. (2004). Introduction to Chemical Engineering Thermodynamics. 7th edition. New York: McGraw-Hill.

Chemical Equilibrium Thermodynamics and Extent of Reaction: Step by Step

Subscribe to our Mailing List!

Featured Posts

A Primer on NAND Flash Memories

Solidification Time and Chvorinov’s Rule

Step-Growth Polymerization, the Carothers Equation, and the Flory-Schulz Distribution

More Articles

Electrode Kinetics and the Tafel Equation

Biomass Gasification

Fields of Study

More

© 2024 Montogue Quiz

Subscribe to
our Mailing List!

Subscribe to our Mailing List!

Subscribe to receive our latest materials in your inbox.

Homework Help

© 2024 Montogue Quiz

Subscribe to our Mailing List!