Nuclear Binding Energy and the Semi-Empirical Mass Formula

In this article, I discuss nuclear binding energy and how it can be represented by a simple empirical relationship first published in the 1930s.

1. The semi-empirical mass formula

Protons and neutrons are commonly referred to as nucleons. They differ in terms of charge – the proton is positively charged whereas the neutron is uncharged – and rest mass – the RM of a neutron is about 1.29 MeV greater than that of a proton. They are bound to the nucleus by the so-called strong nuclear force, which, unlike electrostatic and gravitational forces, is a very short-range force, active at a distance no greater than a few femtometers. At such short distances the strong force is the predominant kind of interaction, exceeding other forces by several orders of magnitude.

Nuclei, the bound states of nucleons, can be contrasted with atoms, the bound states of nuclei and electrons. There is a difference of several orders of magnitude in the typical lengths and energies of these two forms of matter. A typical atom has radius of the order of 10^-10 m (or 1 angstrom), whereas a nucleus is typically measured with lengths of the order of 10^-15 m (or 1 femtometer). Likewise, energetic processes involving atomic orbits only are measured with electron-volts (eV) whereas even the mildest nuclear reactions involve energies of the order of megaelectron-volts (1 MeV = 10⁶ eV).

The binding energy of a nucleus is defined as the negative of the difference between the nuclear mass and the sum of the masses of the constituents:

Here, N is the number of neutrons, m_n is the mass of neutrons, Z is the atomic number, m_p is the mass of a proton, c is the speed of light and B(A,Z) is the binding energy function. Note that B is defined as a positive number: B(A,Z) = –E_B(A,Z), where E_B is the usual (negative) binding energy. Insight on this property can be gained by plotting the average binding energy per nucleon, B/A, as a function of A; such a curve is shown in Figure 1. Several remarkable features are immediately apparent. First of all, the curve is relatively constant except for very light nuclei. The average binding energy of most nuclei is, to within 10%, about 8 MeV per nucleon. Second, we note that the curve reaches a peak near A = 60, where the nuclei are most tightly bound. This suggests that we can “gain” (that is, release) energy in two ways – below A = 60, by assembling lighter nuclei into heavier nuclei, or above A = 60, by breaking heavier nuclei into lighter nuclei. In either case we “climb the curve of binding energy” and liberate nuclear energy; the first process is known as nuclear fusion and the second as nuclear fission.

Figure 1. The binding energy per nucleon.

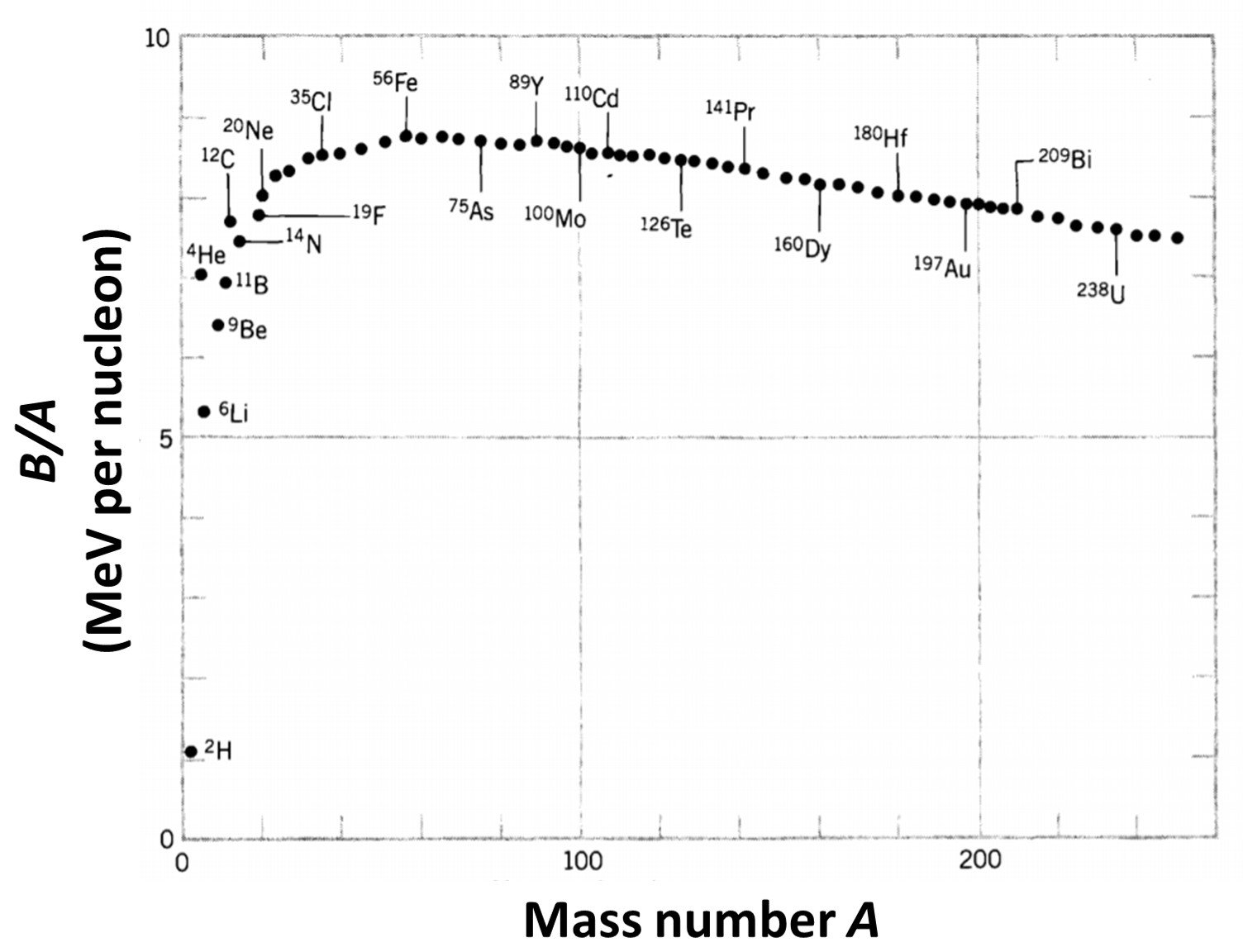
Apart from the lightest elements and a few special very stable nuclei, the binding energy data illustrated in Figure 1 can be approximated by a simple formula containing just a few free parameters. The most well-known fit is the semi-empirical mass formula, first proposed in 1935 by Weizsäcker. It is a “semi”-empirical formula because, although it contains a number of constants that have to be found by fitting experimental data, the formula does have a theoretical basis. This arises from the two properties common to most nuclei (the exceptions are those with very small A values): (I) the interior mass densities are approximately equal, and (II) the total binding energies are approximately proportional to their masses. There is an analogy here with a classical model of a liquid drop, where for drops of various sizes (I) interior densities are the same, and (II) heats of vaporization are proportional to their masses if surface effects are neglected. However, the analogy of a nucleus as an incompressible liquid droplet, with the nucleons playing the role of individual molecules within the droplet, cannot be taken too far because nucleons obey the rules of quantum, not classical, physics.

This SEMF relies on the liquid-drop analogy but also incorporates two quantum ingredients. One is an asymmetry energy that tends to favor equal numbers of protons and neutrons, and the other is a pairing energy that favors configurations where two identical fermions are paired. The binding energy term of the SEMF proposed by Weizsäcker is such that

Coefficients a_i are chosen to give a good approximation to the observed binding energies. A good combination is the following:

Further, (A) is a function of A that depends on the parity of N and Z,

The four terms must be determined empirically (other than a_c, which can be derived from first principles), but their dependence on A and Z reflects simple physical properties that can be explained as follows:

1. Term a_V is a volume term that reflects nearest-neighbor interactions and by itself would contribute a constant binding energy per nucleon B/A  16 MeV. In simple terms, this correction arises from the fact that the strong nuclear force is short-range and each nucleon therefore feels the effect of only the nucleus immediately surrounding it independently of the size of the nucleus. In view of the fact that the nuclear radius is proportional to A^1/3, an immediate consequence is that the binding energy is proportional to the volume, or nuclear mass.

2. Term a_S, which lowers the binding energy, is a surface term. Nucleons on the nuclear surface are surrounded by fewer neighbors and thus are less tightly bound than those in the central region. These nucleons do not contribute to B quite as much as those in the center, and thus B = a_VA overestimates B by giving full weight to the surface nucleons. We must therefore subtract from B a term proportional to the nuclear surface area. The surface area of the nucleus is proportional to R² or to A^2/3, since R  A^1/3. Thus the surface nucleons contribute to the binding energy a term of the form –a_SA^2/3.

3. Term a_C is the Coulomb repulsion term of protons. If we had a uniform spherical charge distribution with a radius proportional to A^1/3, then this term would be proportional to Z² with the constant a_C exactly known. To a very rough approximation, the nucleus can be considered a sphere of uniform charge, but because electrostatic repulsion will only exist for more than one proton, Z² must be replaced by Z(Z – 1), which represents the Coulomb repulsion of the Z(Z – 1)/2 pairs of protons in the nucleus. Then, we may write

4. Term a_A is the asymmetry term. Stable nuclei have Z = A/2. Accordingly, if the binding energy formula is to be realistic in describing the stable nuclei that are actually observed, it must take this effect into account. This term is particularly important for lighter nuclei, for which Z = A/2 is more commonly observed. For heavy nuclei, this term becomes less important, because the rapid increase in the Coulomb repulsion term requires additional neutrons for nuclear stability. A possible form for this term, called the asymmetry or symmetry term because it tends to make the nucleus symmetric in protons and neutrons, is

which has the correct form of favoring nuclei with Z = A/2 and reduces in importance for large A.

5. Finally, we must include another term that accounts for the tendency of the nucleons to couple pairwise to especially stable configurations. When we have an odd number of nucleons (odd Z and even N, or even Z and odd N), this term does not contribute. However, when both Z and N are odd, we gain binding energy by converting one of the odd protons into a neutron (or vice versa) so that it can now form a pair with its formerly odd partner. We find evidence for this pairing force just by looking at the stable nuclei found in nature – there are only four nuclei with odd N and Z (²H, ⁶Li, ¹⁰B, ¹⁴N) but 167 with even N and Z. This pairing term  is usually expressed as +a_PA^-3/4 for Z and N even, –a_PA^-3/4 for Z and A odd, and zero for A odd.

The existence of the Coulomb term and the asymmetry term means that for each A there is a nucleus of maximum binding energy found by setting B/Z = 0. As shown in the next section, the maximally bound nucleus has Z = N = A/2 for low A where the asymmetry term dominates, but the Coulomb term favors N > Z for large A.

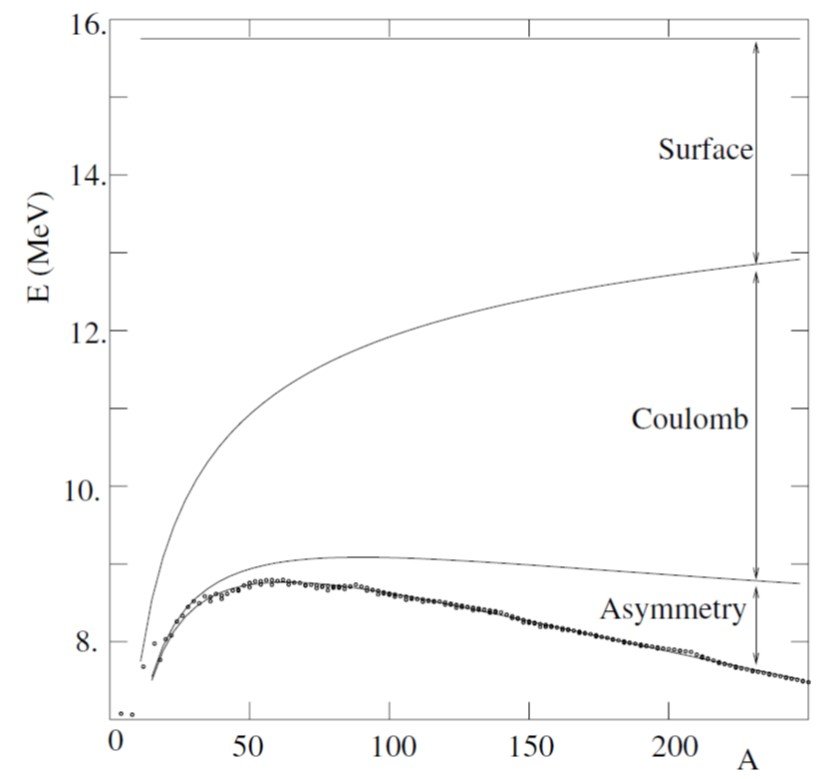
The predicted binding energy for the maximally bound nucleus is shown in Figure 2 as a function of A along the observed binding energies. The figure only shows even-odd nuclei where the pairing term vanishes. The figure also shows the contributions of various terms in the mass formula. We can see that, as A increases, the surface term loses importance in favor of the Coulomb term. The binding energy has a broad maximum in the neighborhood of A  56, which corresponds to the even-Z isotopes of iron and nickel.

  Figure 2. Observed binding energies as a function of A and predictions of the SEMF. For each value of A, the most bound value of Z is used corresponding to Z = A/2 for light nuclei but Z < A/2 for heavy nuclei. Only even-odd combinations of A and Z are considered where the pairing term of the mass formula vanishes. Contributions to the binding energy per nucleon of the various terms in the mass formula are shown. From Basdevant, Rich and Spirro (2005).

2. Applications: Nuclear fission and drip-lines

One simple application of the SEMF is the calculation of the energy released in nuclear fission. In the simple case of symmetric fission of an element (A,Z) into two nuclei (A/2, Z/2), the energy released is

where M’ denotes rest mass. Using a simplified mass equation (replacing Z(Z – 1)  Z² and neglecting the pairing correction ), we obtain

This value becomes positive near A  90 and reaches a value of about 185 MeV for ²³⁶U.

Another application of the SEMF is the prediction of number of nucleons associated with stable states. For a fixed value of A, the nuclear mass becomes a function of its charge alone. Differentiating the SEMF with respect to Z and setting the result to zero, we obtain

To determine whether this stationary point is a minimum or a maximum, we note that

We therefore conclude that the extremum in the foregoing equation corresponds to a minimum. Inspecting the equation for Z_min, we conclude that for low values of A, the minimum in the mass occurs for

which represents the so-called stability line. However, as A increases, the denominator becomes larger than the numerator and we have

where we have used the fact that A = Z + N. As a first approximation, the Z_min formula can be used to predict the most stable nucleus with a given atomic mass number. For a light nucleus such as oxygen, substituting A = 16, we get, noting that (m_n – m_p)c² = 1.29 MeV,

Indeed, the most stable oxygen nucleus is . The formula provides decent estimates for heavier nuclei, too; take lead-208,

This is close to the atomic number of , the most stable isotope of lead.

In much the same spirit of the example above, the SEMF predicts the maximum number of protons for a given N and the maximum number of neutrons for a given Z. The limits are determined by requiring that the last added proton or last added neutron be bound, i.e.

or, in differential terms,

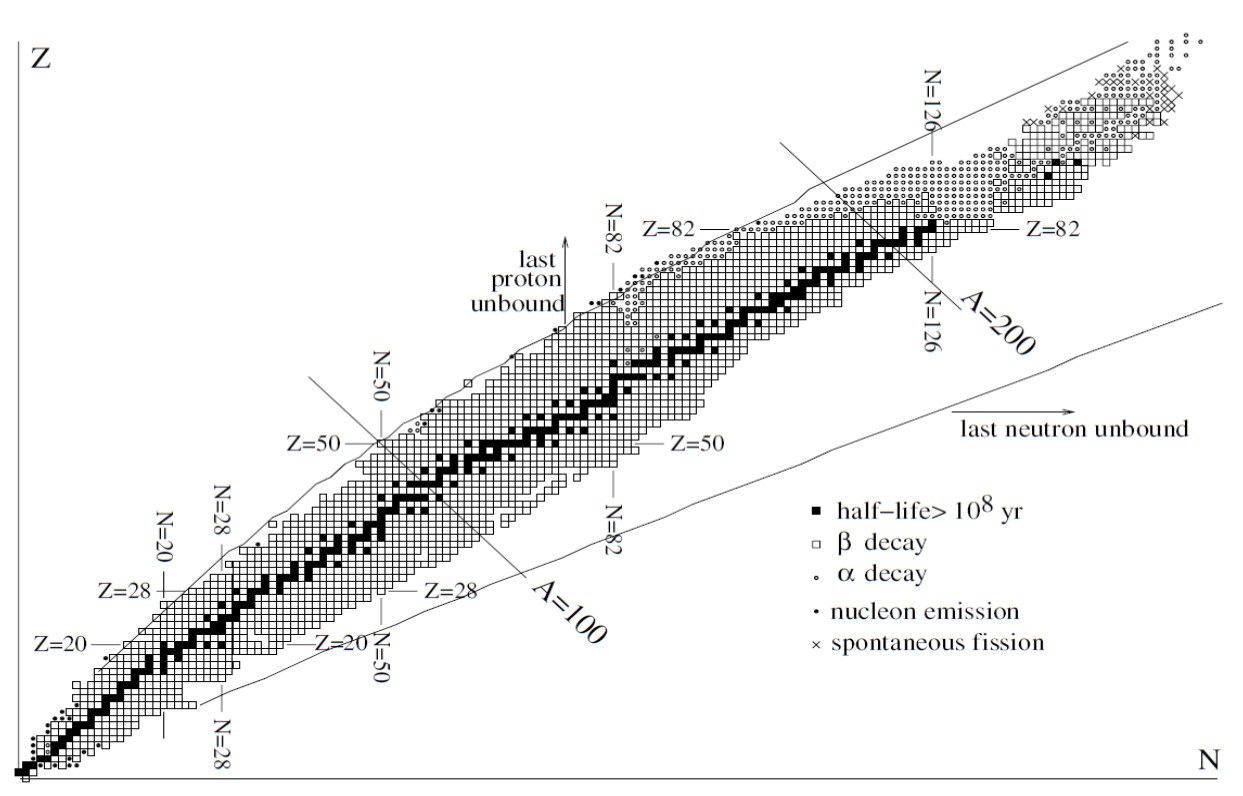
The locus of points (Z, N) where these inequalities become equalities establishes the region where bound states exist. The limits predicted by the mass formula are shown in Figure 3. These lines are called the proton and neutron drip-lines. As expected, some nuclei just outside the drip-lines are observed to decay rapidly by nucleon emission. Combinations of (Z, N) far outside the drip-lines are not observed.

Figure 3. The nuclei. The black squares are long-lived nuclei present on Earth. Combinations of (N, Z) that lie outside the lines marked “last proton/neutron unbound” are predicted to be unbound by the SEMF. Most other nuclei -decay or -decay to long-lived nuclei. From Basdevant, Rich and Spirro (2005).

References

• BASDEVANT, J.-L., RICH, J. and SPIRO, M. (2005). Fundamentals in Nuclear Physics. Berlin/Heidelberg: Springer.

• DAS, A. and FERBEL, T. (2003). Introduction to Nuclear and Particle Physics. 2nd edition. Singapore: World Scientific.

• KRANE, K. (1988). Introductory Nuclear Physics. Hoboken: John Wiley and Sons.

• MARTIN, B. and SHAW, G. (2019) Nuclear and Particle Physics. 3rd edition. Hoboken: John Wiley and Sons.