Tokamaks and the Grad-Shafranov Equation

In this blog post, I provide a quick introduction to the Grad-Shafranov equation, a seminal result in applied fusion physics that describes magnetohydrodynamic (MHD) equilibrium in torus-shaped reactors. In Section 1, I describe two preliminary concepts – a mathematical treatment of the theta-pinch and an introduction to the beta parameter – that will bolster the student’s understanding of the ensuing theory. In Section 2, the Grad-Shafranov equation is derived; the derivation is fairly complicated and requires some background on vector calculus and MHD, but even the unseasoned student will notice, especially from equation (42) onwards, that the theoretical underpinnings of the equation are actually simple. This becomes apparent in Section 3, where an elementary solution of the GS equation is used to derive the vertical magnetic field intensity required to sustain equilibrium in a tokamak. Finally, in Section 4 I present a full-fledged analytical solution to the GS equation and apply it to two real-life tokamaks. The last section is mainly drawn from Freidberg (2014), the closest source I found to Shafranov’s original solution in a 1966 paper published in a volume of Reviews of Plasma Physics. The advanced student is referred to Freidberg’s awesome textbook; Stacey (2005) and Morse (2018) are great, too.

1.Introduction: $\displaystyle \theta$ -pinches and the beta parameter (Boyd and Sanderson, 2003; Freidberg, 2014)

Our starting equation is the lowest-order momentum balance for a plasma under magnetohydrodynamic equilibrium:

$\displaystyle \nabla P=\mathbf{j}\times \mathbf{B}\,\,\,(1)$

That is, the pressure gradient equals the cross product of the current density and magnetic induction vectors. The current and the field must also satisfy Maxwell’s equations

$\displaystyle {{\mu }_{0}}\mathbf{j}=\nabla \times \mathbf{B}\,\,\,(2)$

and

$\displaystyle \nabla \cdot \mathbf{B}=0\,\,\,(3)$

The most immediate consequence of $\displaystyle \nabla P$ = $\displaystyle \mathbf{j}$ $\displaystyle \times$ $\displaystyle \mathbf{B}$ is that the current and magnetic field lie on isobaric surfaces. This follows from the observation that $\displaystyle \mathbf{j}$ • $\displaystyle \nabla P$ = $\displaystyle \mathbf{B}$ • $\displaystyle \nabla P$ = 0 and $\displaystyle \nabla P$ is everywhere normal to the surface P = const. Equation (1) does not imply that $\displaystyle \mathbf{j}$ $\displaystyle \times$ $\displaystyle \mathbf{B}$ is constant on an isobaric surface, since $\displaystyle \nabla P$ will in general vary over an isobaric surface. Equation (1) does state that the force is everywhere normal to the isobaric surface and just balances the pressure gradient force, $\displaystyle -\nabla P$ . Although the current and the magnetic field lie in a common flux surface, they can only be parallel in regions where the pressure gradient vanishes. Since currents that are parallel to the field do not contribute to the force, they are known as “force-free currents.”

The vector product of $\displaystyle \mathbf{B}$ with (1) leads to an expression for the current perpendicular to $\displaystyle \mathbf{B}$ :

$\displaystyle {{\mathbf{j}}_{\bot }}=\frac{{\mathbf{B}\times \nabla P}}{{{{B}^{2}}}}\,\,\,(4)$

We see that there can be no perpendicular current in the absence of a pressure gradient.

The simplest confinement configuration to consider is radial equilibrium of cylindrical plasmas. We assume cylindrical symmetry so that all variables are independent of $\displaystyle \theta$ (azimuthal coordinate) and z (axial coordinate) and the lines of $\displaystyle \mathbf{j}$ and $\displaystyle \mathbf{B}$ lie on surfaces of constant $\displaystyle \mathbf{r}$ . In this case,

$\displaystyle {{\mu }_{0}}\mathbf{j}=\left( {0,\,\,-\frac{{d{{B}_{z}}\left( r \right)}}{{dr}},\,\,\frac{1}{r}\frac{d}{r}\left( {r{{B}_{\theta }}\left( r \right)} \right)} \right)\,\,\,(5)$

and the radial component of the momentum equation yields

$\displaystyle \frac{d}{{dr}}\left[ {P+\frac{{\left( {B_{\theta }^{2}+B_{z}^{2}} \right)}}{{2{{\mu }_{0}}}}} \right]=-\frac{{B_{\theta }^{2}}}{{{{\mu }_{0}}r}}\,\,\,(6)$

which expresses the (radial force) balance between the total (gas + magnetic) pressure gradient and the magnetic tension due to the curvature (if any) of the magnetic field. Of course, it is possible to remove magnetic curvature by choosing $\displaystyle {{B}_{\theta }}$ = 0 so that the gas and magnetic pressure gradients must be oppositely directed and in balance. In this case, setting $\displaystyle {{B}_{\theta }}$ = 0 in equation (6) and integrating, we get

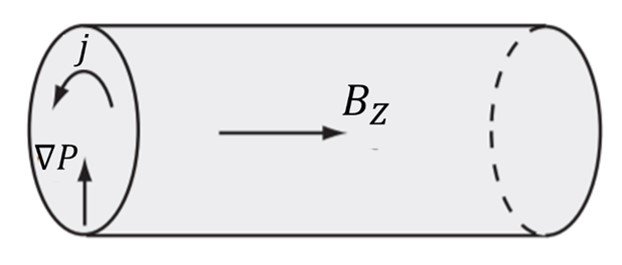
$\displaystyle P*=P+\frac{{{{B}^{2}}}}{{2{{\mu }_{0}}}}=\text{const}\text{.}\,\,\,\text{(7)}$

where P* is total pressure. Such a field can be produced by currents flowing azimuthally; early devices designed to contain plasma in this configuration were known as theta-pinches (since $\displaystyle \theta$ is used to denote the azimuthal coordinate). Azimuthal currents are induced by discharging a current suddenly in a metal conductor enclosing the discharge tube, as illustrated in Figure 1. The induced currents flow in the region between and an axial magnetic field is generated in the region between. The $\displaystyle \mathbf{j}$ $\displaystyle \times$ $\displaystyle \mathbf{B}$ force acts to push the plasma towards the axis until the external magnetic pressure is balanced by the (total) internal pressure; from (7),

$\displaystyle P\left( r \right)+\frac{{{{B}^{2}}\left( r \right)}}{{2{{\mu }_{0}}}}=\frac{{B_{0}^{2}}}{{2{{\mu }_{0}}}}\,\,\,(8)$

where $\displaystyle {{B}_{0}}$ is the external magnetic field. In the absence of any magnetic field there is only the induced field which remains entirely outside the plasma since it cannot penetrate in ideal MHD and (8) reduces to

$\displaystyle P=\frac{{B_{0}^{2}}}{{2{{\mu }_{0}}}}\,\,\,(9)$

i.e., the plasma is radially contained by the magnetic field generated by the azimuthal current flowing in its outer surface. If there is an internal magnetic field B(r), the current penetrates the plasma and (9) applies.

Figure 1. A $\displaystyle \theta$ -pinch.

At this point, it is appropriate to introduce the normalized plasma pressure or beta parameter, a crucial figure of merit not only for the $\displaystyle \theta$ -pinch but all fusion reactor concepts. It measures the efficiency of plasma confinement by the magnetic field and is loosely defined as a ratio of plasma pressure to magnetic pressure,

$\displaystyle \beta =\frac{{\text{Plasma pressure}}}{{\text{Magnetic pressure}}}\,\,\,(10)$

It is customary to define the plasma $\displaystyle \beta$ with respect to the external magnetic field, i.e. $\displaystyle \beta$ = 2 $\displaystyle {{\mu }_{0}}$ $\displaystyle P(r)$ / $\displaystyle B_{0}^{2}$ , so that for a $\displaystyle \theta$ -pinch, from (8),

$\displaystyle \beta \left( r \right)=1-{{\left( {\frac{{B\left( r \right)}}{{{{B}_{0}}}}} \right)}^{2}}\,\,\,(11)$

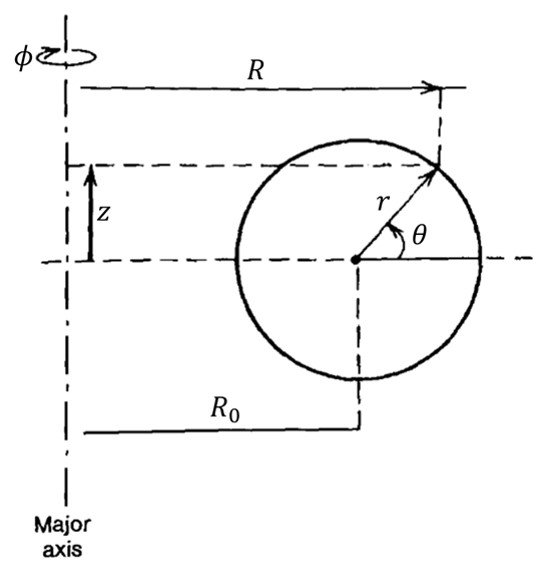
Accordingly, $\displaystyle \beta$ can take any value in the interval 0 < $\displaystyle \beta$ < 1. The simple physics of the $\displaystyle \theta$ -pinch affords a simple equation for the $\displaystyle \beta$ parameter, but more complex concepts imply more complex expressions for (10). The contribution that is to blame for this added complexity usually stems not from the plasma pressure numerator but from the magnetic pressure denominator. For toroid geometries, both the toroidal and poloidal magnetic pressures must be included in the definition; that is, $\displaystyle {{B}^{2}}$ = $\displaystyle B_{t}^{2}$ + $\displaystyle B_{p}^{2}$ . A convenient choice for the toroidal magnetic pressure for any cross-section is to take $\displaystyle B_{t}^{2}$ = $\displaystyle B_{0}^{2}$ as the magnetic induction, where $\displaystyle {{B}_{0}}$ is the vacuum toroidal field at the geometric center of the chamber confining the plasma: R = R₀, as illustrated in Figure 2.

Figure 2. A reference torus cross-section.

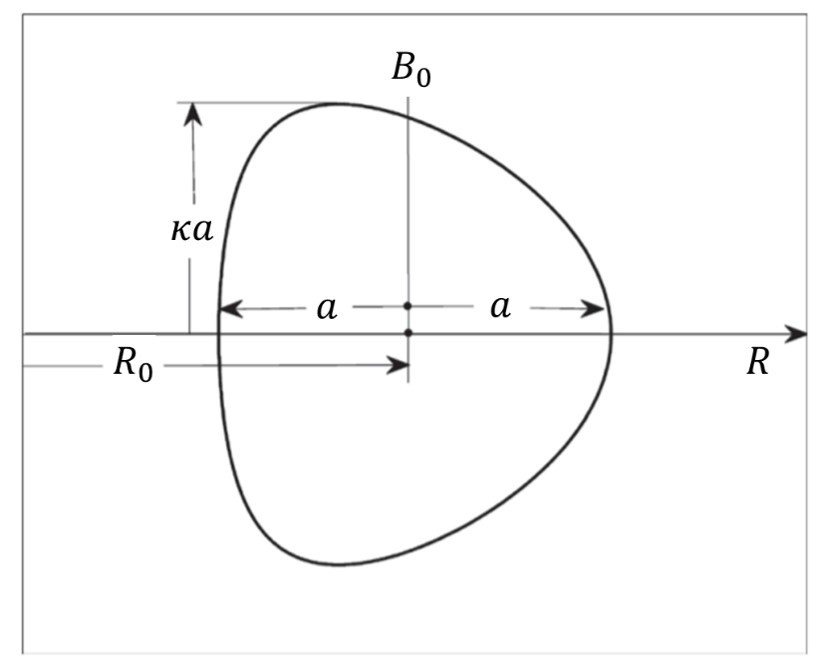
For the poloidal magnetic pressure a good choice for a circular cross-section plasma is $\displaystyle B_{p}^{2}$ = ( $\displaystyle {{\mu }_{0}}I$ / $\displaystyle 2\pi a$ )², where I is the total toroidal plasma current and a is the minor radius of the plasma, also shown in Fig. 2. This definition can be generalized to include noncircular plasmas if we write $\displaystyle B_{p}^{2}$ = ( $\displaystyle {{\mu }_{0}}I$ / $\displaystyle {{C}_{p}}$ )². Here, $\displaystyle {{C}_{p}}$ is the poloidal circumference of the plasma surface, which for simplicity is approximated by

$\displaystyle {{C}_{p}}\approx 2\pi a{{\left( {\frac{{1+{{\kappa }^{2}}}}{2}} \right)}^{{{1}/{2}\;}}}\,\,\,(12)$

where $\displaystyle \kappa$ is the plasma elongation in Fig. 2. To summarize, the definition of $\displaystyle \beta$ adopted for a toroidal geometry is

, $\displaystyle \beta =\frac{{2{{\mu }_{0}}\left\langle P \right\rangle }}{{{{B}^{2}}}}\,\,\,(13)$

where $\displaystyle \left\langle P \right\rangle$ is average plasma pressure and magnetic induction $\displaystyle {{B}^{2}}$ , in accord with our discussion, is conveniently defined as

$\displaystyle {{B}^{2}}=B_{0}^{2}+{{\left( {\frac{{{{\mu }_{0}}I}}{{2\pi a}}} \right)}^{2}}\frac{2}{{1+{{\kappa }^{2}}}}\,\,\,(14)$

It is often useful to define separate toroidal and poloidal $\displaystyle \beta$ s measuring plasma confinement efficiency with respect to each component of the magnetic field. These definitions have the form

$\displaystyle {{\beta }_{t}}=\frac{{2{{\mu }_{0}}\left\langle P \right\rangle }}{{B_{0}^{2}}}\,\,\,(15)$

$\displaystyle {{\beta }_{p}}=\frac{{4{{\pi }^{2}}{{a}^{2}}\left( {1+{{\kappa }^{2}}} \right)\left\langle P \right\rangle }}{{{{\mu }_{0}}{{I}^{2}}}}\,\,\,(16)$

Importantly,

$\displaystyle \frac{1}{\beta }=\frac{1}{{{{\beta }_{t}}}}+\frac{1}{{{{\beta }_{p}}}}\,\,\,(17)$

which indicates that the smaller of the two quantities $\displaystyle {{\beta }_{t}}$ or $\displaystyle {{\beta }_{p}}$ dominates the overall magnetic confinement efficiency.

2.The Grad-Shafranov equation (Stacey, 2005)

Devices such as the $\displaystyle \theta$ -pinch can only contain a plasma radially; there is nothing to prevent the plasma from flowing freely along the field lines and in cylindrical discharges plasma will be lost through the ends of the device unless something is done to prevent this. The obvious answer is to bend the cylinder into a torus so that, rather than flowing out of the ends, the plasma flows round and round the device. This, however, comes at a cost of radial stability, for a cylindrically bent plasma experiences a net outward force due to redistributions of plasma and magnetic pressure. The challenge is to find the optimal mix of poloidal and toroidal fields which can provide toroidal equilibrium without sacrificing radial stability.

The tokamak is the concept of interest in fusion research that has been shown to offer the best combination of toroidal and radial stability. Tokamaks have a large toroidal field and a small poloidal field with an aspect ratio on the order of R₀/a $\displaystyle \sim$ 3. (In tokamak modelling, the so-called major radius R₀ is the distance from the axis of revolution to the centroid of the cross-section, while the so-called minor radius a is the radius of the cross-section itself.) To date, most plasma confinement experiments that enjoyed some degree of success were tokamaks. This includes Princeton’s Tokamak Fusion Test Reactor (TFTR), which in a November 1994 experiment generated 10.7 MW from a 50-50 D-T plasma; the EU’s Joint European Torus (JET), which in 1997 generated 16 MW from a 24 MW input, an efficiency record at the time; and Japan’s JT-60-U, which set a thermal record in 1996 by heating its plasma to 520 MK. Of course, the ITER project, a 5,200-tonne behemoth currently being built in southern France, is also a tokamak. With these case studies in mind, we now turn to a simple mathematical treatment of MHD equilibrium in torus-shaped reactors.

In the following, we consider an axisymmetric, toroidal plasma with a toroidal plasma current. The isobaric surfaces are nested toroidal surfaces, not necessarily with circular cross-section (Figure 3). We define a function $\displaystyle \psi$ = const. for each isobaric surface such that 2 $\displaystyle \pi \psi$ is equal to the poloidal magnetic flux passing through a plane extending from the minor (magnetic) axis out to the isobaric surface and encircling the major axis:

$\displaystyle 2\pi \psi =\int_{{{{S}_{p}}}}{{{{\mathbf{B}}_{p}}\cdot d{{\mathbf{s}}_{P}}}}\,\,\,(18)$

The magnetic axis is the innermost (degenerate) isobaric surface. Recalling that both the current and the field lie in the isobaric surfaces, it follows that the value of $\displaystyle \psi$ is independent of the orientation of the plane, although the area subtended by the plane does depend upon orientation, in general. We will henceforth label the isobaric surfaces according to the corresponding value of $\displaystyle \psi$ and refer to them as flux surfaces.

Figure 3. Toroidal flux surfaces.

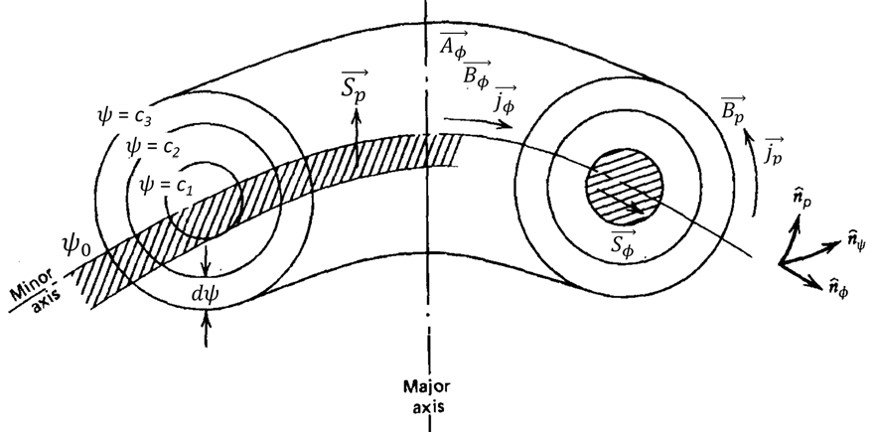
Now consider the incremental poloidal flux between adjacent flux surfaces (i.e., the poloidal flux passing through the planar ribbon extending from the isobaric surface labeled $\displaystyle \psi$ to the isobaric surface labeled $\displaystyle \psi$ + $\displaystyle d\psi$ and encircling the major axis). Note that the separation, $\displaystyle d\psi$ , between adjacent flux surfaces is independent of poloidal orientation, by definition. However, the spatial separation, dr, between adjacent flux surfaces does depend upon the poloidal orientation.

$\displaystyle 2\pi \left( {\psi +d\psi } \right)-2\pi \psi =\int_{{{{S}_{p}}+\delta {{S}_{p}}}}{{{{\mathbf{B}}_{p}}\cdot d{{\mathbf{s}}_{p}}}}-\int_{{{{S}_{p}}}}{{{{\mathbf{B}}_{p}}\cdot d{{\mathbf{s}}_{p}}}}$

$\displaystyle =\int_{{\delta {{S}_{p}}}}{{{{\mathbf{B}}_{p}}\cdot d{{\mathbf{s}}_{p}}}}\approx {{B}_{p}}2\pi Rdr\,\,\,(19)$

where R is the major radius from the major axis to the point in question. Accordingly, we see that

$\displaystyle R{{B}_{p}}=\frac{{d\psi }}{{dr}}=\left| {\nabla \psi } \right|\,\,\,(20)$

We are now able to construct a flux surface coordinate system ( $\displaystyle \psi$ , $\displaystyle \chi$ . $\displaystyle \phi$ ) in which the unit vectors are $\displaystyle {{\mathbf{\hat{n}}}_{\psi }}$ (normal to the flux surface), $\displaystyle {{\mathbf{\hat{n}}}_{p}}$ (in the flux surface and normal to the toroidal direction), and $\displaystyle {{\mathbf{\hat{n}}}_{\phi }}$ (toroidal). Distances in these coordinate directions are $\displaystyle d{{I}_{\psi }}$ = $\displaystyle dr$ = $\displaystyle {{h}_{\psi }}d\psi$ , $\displaystyle d{{I}_{p}}$ , and $\displaystyle d{{I}_{\phi }}$ = $\displaystyle Rd\phi$ = $\displaystyle {{h}_{\phi }}d\phi$ , and the unit vectors are

$\displaystyle {{\mathbf{\hat{n}}}_{\psi }}=\frac{{\nabla \psi }}{{\left| {\nabla \psi } \right|}}=\frac{{\nabla \psi }}{{R{{B}_{p}}}}\,\,\,(21)$

$\displaystyle {{\mathbf{\hat{n}}}_{p}}=\frac{{\nabla \phi \times \nabla \psi }}{{\left| {\nabla \phi \times \nabla \psi } \right|}}=\frac{{\nabla \phi \times \nabla \psi }}{{{{B}_{p}}}}\,\,\,(22)$

and

$\displaystyle {{\mathbf{\hat{n}}}_{\phi }}=\frac{{\nabla \phi }}{{\left| {\nabla \phi } \right|}}=R\nabla \phi \,\,\,(23)$

The volume enclosed by the toroidal flux surface $\displaystyle \psi$ = const. is

$\displaystyle V\left( \psi \right)=\int_{{{{\psi }_{0}}}}^{\psi }{{{{h}_{\psi }}d{\psi }'\oint_{{{\psi }'}}{{d{{I}_{p}}}}\int_{0}^{{2\pi }}{{{{h}_{\phi }}}}d\phi }}=2\pi \int_{{{{\psi }_{0}}}}^{\psi }{{d{\psi }'}}\oint_{{{\psi }'}}{{\frac{{d{{I}_{p}}}}{{{{B}_{p}}}}}}\,\,\,(24)$

and the differential volume of the toroidal annulus between $\displaystyle \psi$ and $\displaystyle \psi$ + $\displaystyle d\psi$ is

$\displaystyle \frac{{dV\left( \psi \right)}}{{d\psi }}d\psi =2\pi d\psi \oint_{\psi }{{\frac{{d{{I}_{P}}}}{{{{B}_{p}}}}\equiv 2\pi {\hat{V}}'\left( \psi \right)d\psi \equiv {V}'\left( \psi \right)d\psi }}\,\,\,(25)$

where $\displaystyle {{\psi }_{0}}$ refers to the magnetic axis. Following Stacey (2005), we hereafter use a prime to denote a derivative with respect to $\displaystyle \psi$ .

Using the results above, the magnetic field can be stated as

$\displaystyle \mathbf{B}={{B}_{\phi }}+{{B}_{p}}=F\nabla \phi +\nabla \phi \times \nabla \psi \,\,\,(26)$

where

$\displaystyle F=R{{B}_{\phi }}\,\,\,(27)$

Because, by definition, $\displaystyle P$ = $\displaystyle P$ ( $\displaystyle \psi$ ), equation (1) can be written in the flux coordinate system as

$\displaystyle {P}'\nabla \psi =\mathbf{j}\times \mathbf{B}\,\,\,(28)$

from which we immediately obtain

$\displaystyle \mathbf{j}\cdot \nabla \psi =\mathbf{B}\cdot \nabla \psi =0\,\,\,(29)$

Using the requirement $\displaystyle \mathbf{j}$ $\displaystyle \cdot$ $\displaystyle \nabla \psi$ and equation (2) brings to

$\displaystyle 0=\left( {\nabla \times \mathbf{B}} \right)\cdot \frac{{\nabla \psi }}{{\left| {\nabla \psi } \right|}}=\frac{1}{{{{h}_{\phi }}}}\frac{\partial }{{\partial {{I}_{p}}}}\left( {{{h}_{\phi }}{{B}_{\phi }}} \right)=\frac{1}{R}\frac{{\partial F}}{{\partial {{I}_{p}}}}\,\,\,(30)$

We know from axisymmetry that $\displaystyle \partial F$ / $\displaystyle \partial \phi$ = 0. Thus, F is a function of flux coordinate $\displaystyle \psi$ only, $\displaystyle R{{B}_{\phi }}$ = $\displaystyle F$ = $\displaystyle F\left( \psi \right)$ .

Using equation (26), the perpendicular current from (4) can be expressed in flux surface coordinates as

$\displaystyle {{\mathbf{j}}_{\bot }}=\frac{{{P}'}}{{{{B}^{2}}}}\left[ {F\left( {\nabla \phi \times \nabla \psi } \right)-{{{\left( {R{{B}_{p}}} \right)}}^{2}}\nabla \phi } \right]\,\,\,(31)$

We conclude immediately that the perpendicular current lies in the flux surface, because $\displaystyle \nabla \psi$ • $\displaystyle {{\mathbf{j}}_{{\bot }}}$ = 0. Thus the total current,

$\displaystyle \mathbf{j}={{\mathbf{j}}_{\bot }}+{{\mathbf{j}}_{{\text{ }\!\!|\!\!\text{ }\,\text{ }\!\!|\!\!\text{ }}}}\,\,\,(32)$

lies in the flux surface, in agreement with our earlier observation. We now write

$\displaystyle {{\mathbf{j}}_{{\text{ }\!\!|\!\!\text{ }\,\text{ }\!\!|\!\!\text{ }}}}={{j}_{{|\,|}}}{{\mathbf{\hat{n}}}_{{|\,|}}}=\frac{{{{j}_{{|\,|}}}\mathbf{B}}}{B}\,\,\,(33)$

and use equations (31) and (32) to obtain

$\displaystyle {{B}_{p}}\frac{\partial }{{\partial {{I}_{P}}}}\left( {\frac{{{{j}_{{|\,|}}}}}{B}+{P}'\frac{F}{{{{B}^{2}}}}} \right)=0\,\,\,(34)$

which indicates that the quantity in brackets is a constant on a flux surface, although it may vary with $\displaystyle \psi$ . We evaluate this constant by taking the flux surface average of the quantity in brackets, after multiplying through by B², to obtain an expression for the current parallel to the magnetic field,

$\displaystyle {{\mathbf{j}}_{{|\,|}}}=\left[ {-\frac{{{P}'F}}{B}\left( {1-\frac{{{{B}^{2}}}}{{\left\langle {{{B}^{2}}} \right\rangle }}} \right)+\frac{{B\left( {{{j}_{{|\,|}}}B} \right)}}{{\left\langle {{{B}^{2}}} \right\rangle }}} \right]{{\mathbf{\hat{n}}}_{{|\,|}}}\,\,\,(35)$

We have defined the flux surface average of a quantity A by

$\displaystyle {{\left\langle A \right\rangle }_{\psi }}\equiv {{\oint_{\psi }{{\frac{{Ad{{I}_{p}}}}{{{{B}_{p}}}}}}}}/{{\oint_{\psi }{{\frac{{d{{I}_{p}}}}{{{{B}_{p}}}}}}}}\;={{\oint_{\psi }{{\frac{{Ad{{I}_{p}}}}{{{{B}_{p}}}}}}}}/{{{V}'\left( \psi \right)}}\;\,\,\,(36)$

(We suppress the $\displaystyle \psi$ subscript for clarity.) Equation (35) contains an unknown constant, $\displaystyle \left\langle {{{j}_{{\text{II}}}}B} \right\rangle$ , that must be evaluated from more fundamental considerations involving the mass flow of the plasma.

We can construct the toroidal and poloidal currents in the flux surface, (31) and (35),

$\displaystyle {{j}_{\phi }}\equiv {{\mathbf{\hat{n}}}_{\phi }}\cdot {{\mathbf{j}}_{\bot }}+{{\mathbf{\hat{n}}}_{\phi }}\cdot {{\mathbf{j}}_{{|\,|}}}=-R\left( {1-\frac{{B_{\phi }^{2}}}{{\left\langle {{{B}^{2}}} \right\rangle }}} \right){P}'+\frac{{{{B}_{\phi }}\left\langle {{{j}_{{|\,|}}}B} \right\rangle }}{{\left\langle {{{B}^{2}}} \right\rangle }}\,\,\,(37)$

and

$\displaystyle {{j}_{p}}={{\mathbf{\hat{n}}}_{p}}\cdot {{\mathbf{j}}_{\bot }}+{{\mathbf{\hat{n}}}_{p}}\cdot {{\mathbf{j}}_{{|\,|}}}=\frac{{{{B}_{P}}F{P}'}}{{\left\langle {{{B}^{2}}} \right\rangle }}+\frac{{{{B}_{P}}\left\langle {{{j}_{{|\,|}}}B} \right\rangle }}{{\left\langle {{{B}^{2}}} \right\rangle }}\,\,\,(38)$

These currents must be consistent with Ampère’s law. The toroidal and poloidal components of equation (2), in flux surface coordinates, are

$\displaystyle {{j}_{\phi }}=\frac{R}{{{{\mu }_{0}}}}\nabla \cdot {{R}^{{-2}}}\nabla \psi \,\,\,(39)$

and

$\displaystyle {{j}_{p}}=-\frac{{{{B}_{P}}}}{{{{\mu }_{0}}}}{F}'\,\,\,(40)$

Equating (38) and (40) results in the equation that must be satisfied by $\displaystyle F\left( \psi \right)$ ,

$\displaystyle {F}'=-{{\mu }_{0}}\left( {\frac{{F{P}'}}{{\left\langle {{{B}^{2}}} \right\rangle }}+\frac{{\left\langle {{{j}_{{|\,|}}}B} \right\rangle }}{{\left\langle {{{B}^{2}}} \right\rangle }}} \right)\,\,\,(41)$

Equating (37) and (39) and using (41) ultimately leads to

$\displaystyle \nabla \cdot {{R}^{{-2}}}\nabla \psi +F\left( \psi \right){F}'\left( \psi \right)+{{\mu }_{0}}{{R}^{2}}{P}'\left( \psi \right)=0\,\,\,(42)$

This general expression for axisymmetric, toroidal equilibria is known as the Grad-Shafranov equation. It is a nonlinear partial differential equation derived from the ideal MHD equations for static, toroidal equilibria with azimuthal symmetry ( $\displaystyle \partial$ / $\displaystyle \partial \phi$ = 0) for the flux function $\displaystyle \psi$ , which determines the poloidal magnetic field. It expresses the balance between plasma pressure gradient (third term) and the $\displaystyle \mathbf{j}$ $\displaystyle \times$ $\displaystyle \mathbf{B}$ contributions (first and second terms). Of the latter, the first term represents the toroidal current and poloidal field, which we identified as essential for toroidal stability, and the second term comes from the poloidal current and toroidal field determining radial stability. Indeed, it is easy to see that if we drop the first term in equation (42), integrate, and use the relationships developed heretofore, we recover (7), the equation for radial equilibrium in a $\displaystyle \theta$ -pinch.

Solutions to the Grad-Shafranov equation provide a complete characterization of axisymmetric ideal MHD equilibria. The nature of the equilibrium configuration is determined by the choice of the two arbitrary functions $\displaystyle P\left( \psi \right)$ and $\displaystyle F\left( \psi \right)$ for the pressure and current profiles, respectively, together with the boundary conditions. Given P and F, equation (42) is solved as a boundary value problem to find the flux function $\displaystyle \psi \left( {R,Z} \right)$ . The main difficulty lies in the fact that P and F are themselves functions of $\displaystyle \psi$ , which is not known until (42) is solved.

3.Asymptotic solutions and the vertical magnetic field (Stacey, 2005)

Although in practice solution of the Grad-Shafranov equation for magnetic flux surfaces is carried out numerically, it is useful to develop an approximate solution that provides significant physical insight. With this purpose in mind, we take the inverse aspect ratio

$\displaystyle \varepsilon \equiv \frac{a}{{{{R}_{0}}}}\ll 1$

where R₀ and a are the major and minor radii of the plasma, respectively. Conceptually, the plasma geometry in this case is more akin to a bicycle tire than a donut.

The solution of (42) for the flux surface function, $\displaystyle \psi$ , outside the plasma surface can be written in a form that is independent of the current and pressure distributions within the plasma. In a toroidal ( $\displaystyle r$ , $\displaystyle \theta$ , $\displaystyle \phi$ ) coordinate system, the solution is

$\displaystyle 2\pi \psi \left( {r,\theta } \right)=-{{\mu }_{0}}IR\left[ {\ln \left( {\frac{{8R}}{r}} \right)-2} \right]+\left\{ {-\frac{1}{2}{{\mu }_{0}}I\left[ {\ln \left( {\frac{{8R}}{r}} \right)-1} \right]r+\frac{{{{c}_{1}}}}{r}+{{c}_{2}}r} \right\}\cos \theta \,\,\,(43)$

with r $\displaystyle \ge$ a. Here, I is the total toroidal plasma current and c₁ and c₂ are constants to be determined. In this approximation, the flux surfaces are circles with centers that are displaced from the minor axis (r = 0) by

$\displaystyle \Delta \left( r \right)=-\frac{{{{r}^{2}}}}{{2R}}\left[ {\ln \left( {\frac{{8R}}{r}} \right)-1} \right]+\frac{1}{{{{\mu }_{0}}IR}}\left( {{{c}_{1}}+{{c}_{2}}{{r}^{2}}} \right)\,\,\,(44)$

Now, the magnetic field in the $\displaystyle r$ – $\displaystyle \theta$ plane can be derived from

$\displaystyle \mathbf{B}=\nabla \times \left( {\frac{\psi }{R}} \right){{\mathbf{\hat{n}}}_{\phi }}\,\,\,(45)$

Thus, the field outside the plasma is

$\displaystyle {{B}_{\theta }}=\frac{1}{R}\frac{{\partial \psi }}{{\partial r}}$

$\displaystyle \therefore {{B}_{\theta }}=\frac{1}{{2\pi }}\left\{ {\frac{{{{\mu }_{0}}I}}{r}+\frac{1}{R}\left[ {-\frac{1}{2}{{\mu }_{0}}I\ln \left( {\frac{{8R}}{r}} \right)-\frac{{{{c}_{1}}}}{{{{r}^{2}}}}+{{c}_{2}}} \right]\cos \theta } \right\}\,\,\,(46)$

and

$\displaystyle {{B}_{r}}=-\frac{1}{R}\frac{{\partial \psi }}{{\partial \theta }}$

$\displaystyle \therefore {{B}_{r}}=\frac{1}{{2\pi R}}\left\{ {-\frac{1}{2}{{\mu }_{0}}I\left[ {\ln \left( {\frac{{8R}}{r}} \right)-1} \right]+\frac{{{{c}_{1}}}}{{{{r}^{2}}}}+{{c}_{2}}} \right\}\sin \theta \,\,\,(47)$

This model can help us understand the confinement properties of toroidal plasmas. If the flux function is due entirely to the current flowing in the plasma – that is, there are no external fields – then the natural boundary condition $\displaystyle \psi$ ( $\displaystyle r\to \infty$ ) $\displaystyle \to$ 0 requires that c₂ = 0. The other boundary condition on $\displaystyle \psi$ , at the plasma surface r = a, is that the normal component of the magnetic field at r = a shoud vanish because the plasma boundary is a flux surface. Requiring $\displaystyle {{B}_{r}}$ (r = a) = 0 in equation (47) leads to

$\displaystyle {{c}_{1}}=\frac{{{{\mu }_{0}}I}}{{2{{a}^{2}}}}\left[ {\ln \left( {\frac{{8R}}{a}} \right)-1} \right]\,\,\,(48)$

In this case, equation (46) evaluated at the plasma surface is

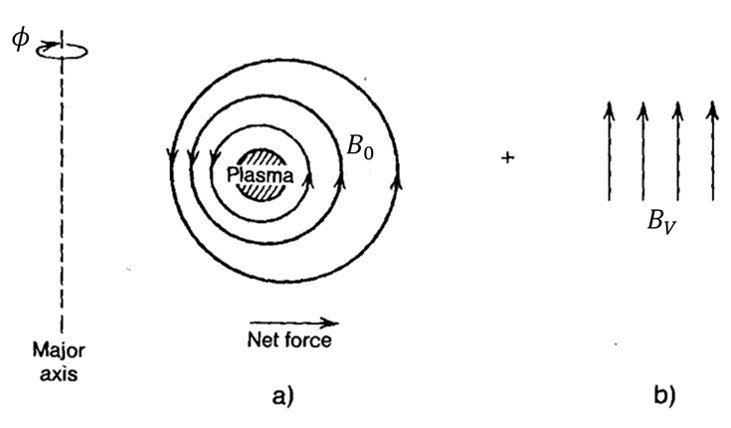
$\displaystyle {{B}_{\theta }}\left( {a,\theta } \right)=\frac{{{{\mu }_{0}}I}}{{2\pi a}}\left\{ {1-\frac{a}{R}\left[ {\ln \left( {\frac{{8R}}{a}} \right)-\frac{1}{2}} \right]\cos \theta } \right\}\,\,\,(49)$

If we now make the assumption that the plasma is a perfect conductor, we can arrive at some useful qualitative insights. Since there is no magnetic field within a perfect conductor, the magnetic pressure $\displaystyle B_{p}^{2}$ / $\displaystyle 2{{\mu }_{0}}$ just outside the plasma surface must be balanced by the plasma kinetic pressure $\displaystyle P(a)$ just inside the plasma surface. Because the plasma pressure is constant on a flux surface and the plasma surface is a flux surface, the kinetic pressure is uniform around the plasma surface 0 $\displaystyle \le$ $\displaystyle \theta$ $\displaystyle \le$ 2 $\displaystyle \pi$ . However, the magnetic pressure is obviously (equation (49)) nonuniform around the plasma surface, being stronger on the inside at $\displaystyle \theta$ = $\displaystyle \pi$ than on the outside at $\displaystyle \theta$ = 0, as illustrated in Figure 4a. Thus if the plasma and magnetic pressures were balanced on the average, there would be a net force on the plasma directed radially outward. It is necessary to eliminate this net force by adding a vertical field, as indicated in Fig. 4b, to strengthen the poloidal field on the outside of the torus ( $\displaystyle \theta$ = 0) and to weaken the poloidal field on the inside of the torus ( $\displaystyle \theta$ = $\displaystyle \pi$ ). This vertical field, $\displaystyle {{B}_{V}}$ , must be provided by coils or a conducting shell located external to the plasma.

Figure 4. Magnetic fields affecting plasma equilibrium.

Now, we reformulate the solution under the assumption that the approximate solution to the GS equation given by (43) consists of a component due to the currents in the external coils or conducting shell and a component due to the plasma,

$\displaystyle {{\psi }_{p}}=\psi -{{\psi }_{e}}\,\,\,(50)$

where

$\displaystyle {{\psi }_{e}}={{c}_{2}}r\cos \theta \,\,\,(51)$

The constants c₁ and c₂ are now determined by requiring that the normal component of the field ( $\displaystyle {{B}_{r}}$ ) vanishes at the plasma surface and that the tangential component of the field ( $\displaystyle {{B}_{\theta }}$ ) is continuous across the plasma surface. At this point we define the plasma internal inductance $\displaystyle {{\ell }_{i}}$ per unit length, a dimensionless quantity given by

$\displaystyle {{\ell }_{i}}=\int_{0}^{{2\pi }}{{d\theta }}\int_{0}^{a}{{\left( {\frac{{B_{\theta }^{2}r}}{{\pi {{a}^{2}}{{{\left\langle {B_{\theta }^{2}} \right\rangle }}_{{{{\psi }_{a}}}}}}}} \right)dr}}\,\,\,(52)$

We likewise define a quantity $\displaystyle \Lambda$ , sometimes known as the plasma parameter,

$\displaystyle \Lambda ={{\beta }_{p}}+\frac{1}{2}{{\ell }_{i}}-1\,\,\,(53)$

Accordingly, the flux surface functions outside the plasma can be written

$\displaystyle 2\pi {{\psi }_{e}}=\frac{{{{\mu }_{0}}I}}{2}\left[ {\ln \left( {\frac{{8{{R}_{0}}}}{a}} \right)+\Lambda -\frac{1}{2}} \right]r\cos \theta \,\,\,(54)$

and

$\displaystyle 2\pi {{\psi }_{p}}=-{{\mu }_{0}}I{{R}_{0}}\left[ {\ln \left( {\frac{{8{{R}_{0}}}}{r}} \right)-2} \right]+\frac{1}{2}{{\mu }_{0}}I\left[ {-\ln \left( {\frac{{8{{R}_{0}}}}{r}} \right)+1-\frac{{{{a}^{2}}}}{{{{r}^{2}}}}\left( {\Lambda +\frac{1}{2}} \right)} \right]r\cos \theta \,\,\,(55)$

The components of the field due to the external coils in an ( $\displaystyle R$ , $\displaystyle Z$ , $\displaystyle \phi$ ) coordinate system, with Z the direction along the major axis measured relative to the horizontal symmetry plane, are

$\displaystyle {{B}_{{V,R}}}=\frac{1}{R}\frac{{\partial {{\psi }_{e}}}}{{\partial z}}=-\frac{{{{\mu }_{0}}I}}{{4\pi R}}\left[ {\ln \left( {\frac{{8{{R}_{0}}}}{a}} \right)+\Lambda -\frac{1}{2}} \right]\tan \theta \,\,\,\left( {r>a} \right)\,\,\,(56)$

and

$\displaystyle {{B}_{{V,Z}}}=\frac{1}{R}\frac{{\partial {{\psi }_{e}}}}{{\partial R}}=\frac{{{{\mu }_{0}}I}}{{4\pi R}}\left[ {\ln \left( {\frac{{8{{R}_{0}}}}{a}} \right)+\Lambda -\frac{1}{2}} \right]\,\,\,\left( {r>a} \right)\,\,\,(57)$

where we have made use of the relationships (see Figure 5)

$\displaystyle R={{R}_{0}}+r\cos \theta \,\,\,(58)$

$\displaystyle z=r\sin \theta \,\,\,(59)$

Formulas (56) and (57) provide valuable information about the design requirements for the vertical field circuit, in particular how large the vertical field must be to center the plasma as a function of toroidal current and geometry.

Figure 5. Relation of ( $\displaystyle R$ , $\displaystyle z$ , $\displaystyle \theta$ ) and toroidal ( $\displaystyle r$ , $\displaystyle \theta$ , $\displaystyle \phi$ ) coordinate systems.

4.Analytic solution (Freidberg, 2014)

As shown in the previous section, use of asymptotic expansions in small $\displaystyle \varepsilon$ has proven useful for developing intuition about the vertical magnetic field required to sustain magnetohydrodynamic equilibrium in a tokamak. As shown in Freidberg (2014), low approximations can also be used to analyze ohmic and elliptic tokamaks, including calculation of simple analytic profiles for figures of merit such as the beta parameter. For a standard tokamak, however, the inverse aspect ratio is high enough ( $\displaystyle \varepsilon$ $\displaystyle \sim$ 1/3) that an asymptotic solution yields prohibitively inaccurate results. The situation is even more difficult for the ultra-tight aspect ratio spherical tokamak, which has $\displaystyle \varepsilon$ $\displaystyle \sim$ 3/4. The implication is that for high accuracy MHD applications to experiment, one must resort to the “exact” solutions to the Grad-Shafranov equation, or at best a very precise numerical procedure. For the latter approach, many such codes are in existence today. Although the numerical solutions are essential for detailed experimental comparisons, they are not as convenient for developing simple scaling laws describing the effects of aspect ratio, elongation, and triangularity on tokamak equilibria. In other words, it would be desirable if in addition to the numerical codes there existed analytical solutions to the Grad-Shafranov equation. Developing one such solution is the final goal of this article.

Following Freidberg (2014), we denote the free functions F and P in such a manner that

$\displaystyle F\left( {\frac{{dF}}{{d\psi }}} \right)=-A\,\,\,;\,\,\,{{\mu }_{0}}\left( {\frac{{dP}}{{d\psi }}} \right)=-C\,\,(60,61)$

where A and C are constants. The surfaces defined by (60) and (61) are known as Solov’ev profiles. With these choices the Grad-Shafranov equation becomes

$\displaystyle R\frac{\partial }{{\partial R}}\left( {\frac{1}{R}\frac{{\partial \psi }}{{\partial R}}} \right)+\frac{{{{\partial }^{2}}\psi }}{{\partial {{Z}^{2}}}}=A+C{{R}^{2}}\,\,\,(62)$

At this point it is useful to normalize the flux function and the coordinates as follows: $\displaystyle R$ = $\displaystyle {{R}_{0}}X$ , $\displaystyle Z$ = $\displaystyle {{R}_{0}}Y$ , $\displaystyle \psi$ = $\displaystyle {{\psi }_{0}}U$ where $\displaystyle {{\psi }_{0}}$ = $\displaystyle R_{0}^{2}$ ( $\displaystyle A$ + $\displaystyle CR_{0}^{2}$ ). The signs are chosen so that $\displaystyle {{\psi }_{0}}$ > 0 and $\displaystyle U(X,Y)$ < 0. The Grad-Shafranov equation reduces to

$\displaystyle X\frac{\partial }{{\partial X}}\left( {\frac{1}{X}\frac{{\partial U}}{{\partial X}}} \right)+\frac{{{{\partial }^{2}}U}}{{\partial {{Y}^{2}}}}=\alpha +\left( {1-\alpha } \right){{X}^{2}}\,\,\,(63)$

Here, $\displaystyle \alpha$ = $\displaystyle A$ /( $\displaystyle A$ + $\displaystyle CR_{0}^{2}$ ). Effectively $\displaystyle \alpha$ and $\displaystyle {{\psi }_{0}}$ have replaced A and C as the free parameters. The advantage of this normalization is that the differential equation itself is now a function of a single parameter, $\displaystyle \alpha$ .

There is now a crucial difference in the way that the exact equation is solved as compared to the asymptotic approach. In the latter, a standard approach is used. A surface is specified, for instance a circle or ellipse, and the equations are solved subject to the boundary conditions of regularity and $\displaystyle \psi$ = 0 on the surface.

This approach does not really work for the exact problem because simple analytic solutions cannot be found that exactly satisfy the boundary conditions on simple surfaces such as a circle or an ellipse. Instead, the approach used is to find an exact analytic solution to equation (62) consisting of the superposition of a finite number of terms each with an undetermined multiplicative amplitude. A series of boundary constraints is then applied, forcing the analytic solutions to match a finite number of specified conditions on a known desired surface – one boundary constraint for each unknown multiplicative amplitude. The resulting solution is then uniquely defined. One then simply plots the contours of U = constant, including the plasma surface U = 0. Obviously, matching properties at a finite number of points does not guarantee that the resulting U = 0 surface will be close to the desired matching surface at all points. One must just take whatever the solution produces. The mathematical challenges to make this approach work involve choosing (1) the right set of analytic basis functions, (2) the right number of terms in the finite sum, and (3) the right set of matching constraints, so that the resulting U = 0 surface closely matches the desired surface for a very wide range of plasma parameters.

The solution to (62) consists of particular and homogeneous contributions. A convenient way to write the particular solution is the following:

$\displaystyle {{U}_{P}}\left( {X,Y} \right)=\frac{\alpha }{2}{{X}^{2}}\ln X+\frac{{1-\alpha }}{8}{{X}^{4}}\,\,\,(64)$

The homogeneous solution, in turn, satisfies

$\displaystyle X\frac{\partial }{{\partial X}}\left( {\frac{1}{X}\frac{{\partial {{U}_{H}}}}{{\partial X}}} \right)+\frac{{{{\partial }^{2}}{{U}_{H}}}}{{\partial {{Y}^{2}}}}=0\,\,\,(65)$

Simple basis functions that exactly satisfy (62) consist of combinations of polynomials in X and Y. The exact form of each polynomial solution can be easily found by direct substitution. The approach used here assumes that the overall solution can be written as a Taylor series in these polynomial solutions, starting from a constant and increasing up to and including sixth-order terms. Truncating the series at sixth-order polynomials is not an obvious choice and indeed was arrived at by trial and error. At any rate, the exact analytic solution to the Grad-Shafranov equation used to model tokamaks is given by

$\displaystyle U\left( {X,Y} \right)=\frac{\alpha }{2}{{X}^{2}}\ln X+\frac{{1-\alpha }}{8}{{X}^{4}}+\sum\limits_{0}^{6}{{{{c}_{j}}{{U}_{j}}}}\,\,\,(66)$

$\displaystyle 1.\,{{U}_{0}}=1$

$\displaystyle 2.\,{{U}_{1}}={{X}^{2}}$

$\displaystyle 3.\,{{U}_{2}}={{Y}^{2}}-{{X}^{2}}\ln X$

$\displaystyle 4.\,{{U}_{3}}={{X}^{4}}-4{{X}^{2}}{{Y}^{2}}$

$\displaystyle 5.\,{{U}_{4}}=2{{Y}^{4}}-9{{Y}^{2}}{{X}^{2}}-\left( {12{{Y}^{2}}{{X}^{2}}-3{{X}^{4}}} \right)\ln X$

$\displaystyle 6.\,{{U}_{5}}={{X}^{6}}-12{{X}^{4}}{{Y}^{2}}+8{{X}^{2}}{{Y}^{4}}$

$\displaystyle 7.\,{{U}_{6}}=8{{Y}^{6}}-140{{Y}^{4}}{{X}^{2}}+75{{Y}^{2}}{{X}^{4}}-\left( {120{{Y}^{4}}{{X}^{2}}-180{{Y}^{2}}{{X}^{4}}+15{{X}^{6}}} \right)\ln X$

Observe that all the polynomials are even in Y, indicating that attention is focused on up-down symmetric configurations.

The task now is to define seven boundary constraints that will serve to determine the seven unknown coefficients c_j. These constraints are chosen to match seven properties on a known desired plasma surface. A good choice for this reference surface, which is often used in the fusion community, is given parametrically in terms of variable $\displaystyle \tau$ as

$\displaystyle X=1+\varepsilon \cos \left( {\tau +{{\delta }_{0}}\sin \tau } \right)\,\,\,(67)$

$\displaystyle Y=\varepsilon \kappa \sin \tau \,\,\,(68)$

The surface and corresponding geometry are illustrated in Figure 6. As can be seen, eqs. (67) and (68) parametrize a “D” shaped contour in terms of three dimensionless parameters: the inverse aspect ratio $\displaystyle \varepsilon$ = $\displaystyle a$ / $\displaystyle {{R}_{0}}$ , the elongation $\displaystyle \kappa$ , and the triangularity $\displaystyle \delta$ = sin $\displaystyle {{\delta }_{0}}$ . The boundary constraints, again found by some trial and error, require matching the analytic flux function and its first and second derivatives at three separate points on the reference surface: the outer equatorial point, the inner equatorial point, and the high point maximum. This might appear to correspond to nine constraints but two are already satisfied – the first derivative conditions at the outer and inner equatorial points by virtue of up-down symmetry. Seven boundary conditions remain, namely:

$\displaystyle 1.\,U\left( {1+\varepsilon ,0} \right)=0\,(\text{outer point flux)}$

$\displaystyle 2.\,{{U}_{{YY}}}\left( {1+\varepsilon ,0} \right)=-{{N}_{1}}{{U}_{X}}\left( {1+\varepsilon ,0} \right)\,\,(\text{outer point curvature)}$

$\displaystyle 3.\,U\left( {1-\varepsilon ,0} \right)=0\,\,(\text{inner point flux)}$

$\displaystyle 4.\,{{U}_{{YY}}}\left( {1-\varepsilon ,0} \right)=-{{N}_{2}}{{U}_{X}}\left( {1-\varepsilon ,0} \right)\,\,(\text{inner point curvature)}$

$\displaystyle 5.\,U\left( {1-\delta \varepsilon ,\kappa \varepsilon } \right)=0\,\,(\text{high point flux)}$

$\displaystyle 6.\,{{U}_{X}}\left( {1-\delta \varepsilon ,\kappa \varepsilon } \right)=0\,\,(\text{high point slope)}$

$\displaystyle 7.\,{{U}_{{XX}}}\left( {1-\delta \varepsilon ,\kappa \varepsilon } \right)=-{{N}_{3}}{{U}_{Y}}\left( {1-\delta \varepsilon ,\kappa \varepsilon } \right)\,\,(\text{high point curvature)}$

Here, N_j are curvature coefficients that can be determined from the model surface,

$\displaystyle {{N}_{1}}={{\left. {\frac{{{{d}^{2}}X}}{{d{{Y}^{2}}}}} \right|}_{{\tau =0}}}=\frac{{{{{\left( {1+{{\delta }_{0}}} \right)}}^{2}}}}{{\varepsilon {{\kappa }^{2}}}}\,\,\,(69)$

$\displaystyle {{N}_{2}}={{\left. {\frac{{{{d}^{2}}X}}{{d{{Y}^{2}}}}} \right|}_{{\tau =\pi }}}=-\frac{{{{{\left( {1-{{\delta }_{0}}} \right)}}^{2}}}}{{\varepsilon {{\kappa }^{2}}}}\,\,\,(70)$

$\displaystyle {{N}_{3}}={{\left. {\frac{{{{d}^{2}}X}}{{d{{Y}^{2}}}}} \right|}_{{\tau ={\pi }/{2}\;}}}=-\frac{\kappa }{{\varepsilon {{{\cos }}^{2}}{{\delta }_{0}}}}\,\,\,(71)$

Once the free constants A and C or, equivalently, $\displaystyle \alpha$ and $\displaystyle {{\psi }_{0}}$ are specified, the constraint conditions given by 1 to 7 constitute a set of seven linear inhomogeneous algebraic equations for the seven unknown coefficients c_i, a trivial numerical problem.

The last step in the formulation is to derive relationships for the figures of merit q_* (the kink safety factor), $\displaystyle {{\beta }_{t}}$ (the poloidal beta), and $\displaystyle {{\beta }_{p}}$ (the toroidal beta), which can be shown to depend on $\displaystyle \alpha$ , $\displaystyle {{\psi }_{0}}$ , and the geometry of the section:

$\displaystyle \frac{1}{{{{q}_{*}}}}=\frac{1}{{2\pi }}\left( {\frac{2}{{1+{{\kappa }^{2}}}}} \right)\left( {\frac{{{{\psi }_{0}}}}{{{{a}^{2}}{{B}_{0}}}}} \right){{K}_{1}}\,\,\,(72)$

$\displaystyle {{\beta }_{p}}=8{{\pi }^{2}}{{\varepsilon }^{2}}\left( {1-\alpha } \right)\left( {\frac{{1+{{\kappa }^{2}}}}{2}} \right)\frac{{{{K}_{2}}}}{{K_{1}^{2}{{K}_{3}}}}\,\,\,(73)$

$\displaystyle {{\beta }_{t}}=\left[ {\frac{{8{{\pi }^{2}}{{\varepsilon }^{4}}\left( {1-\alpha } \right)}}{{q_{*}^{2}}}} \right]{{\left( {\frac{{1+{{\kappa }^{2}}}}{2}} \right)}^{2}}\frac{{{{K}_{2}}}}{{K_{1}^{2}{{K}_{3}}}}\,\,\,(74)$

where

$\displaystyle {{K}_{1}}=\int{{dXdY\left[ {\frac{{\alpha +\left( {1-\alpha } \right){{X}^{2}}}}{X}} \right]}}\,\,\,(75)$

$\displaystyle {{K}_{2}}=\int{{XdXdY\left( {-U} \right)}}\,\,\,(76)$

$\displaystyle {{K}_{3}}=\int{{XdXdY}}\,\,\,(77)$

Figure 6. Geometry of the reference surface.

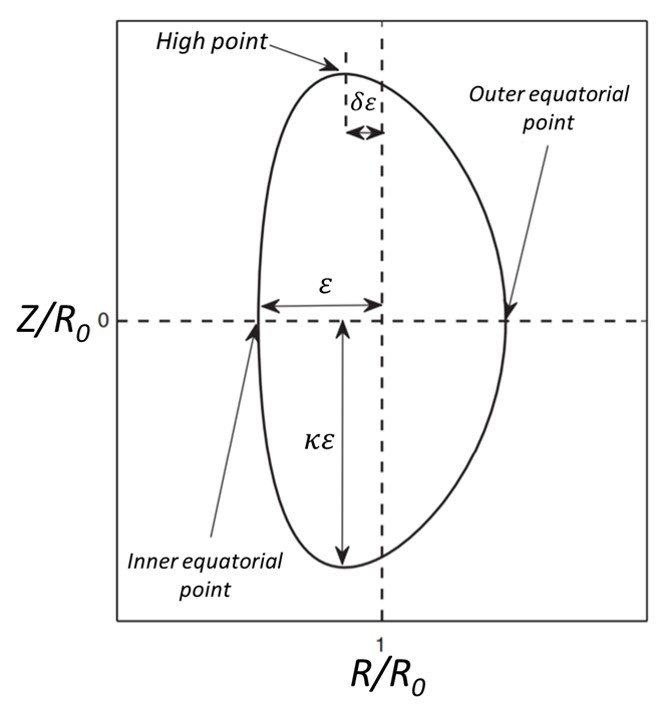
Table 1 summarizes characteristics of the TFTR and JET tokamaks.

Table 1. Characteristics of the TFTR and JET tokamaks.

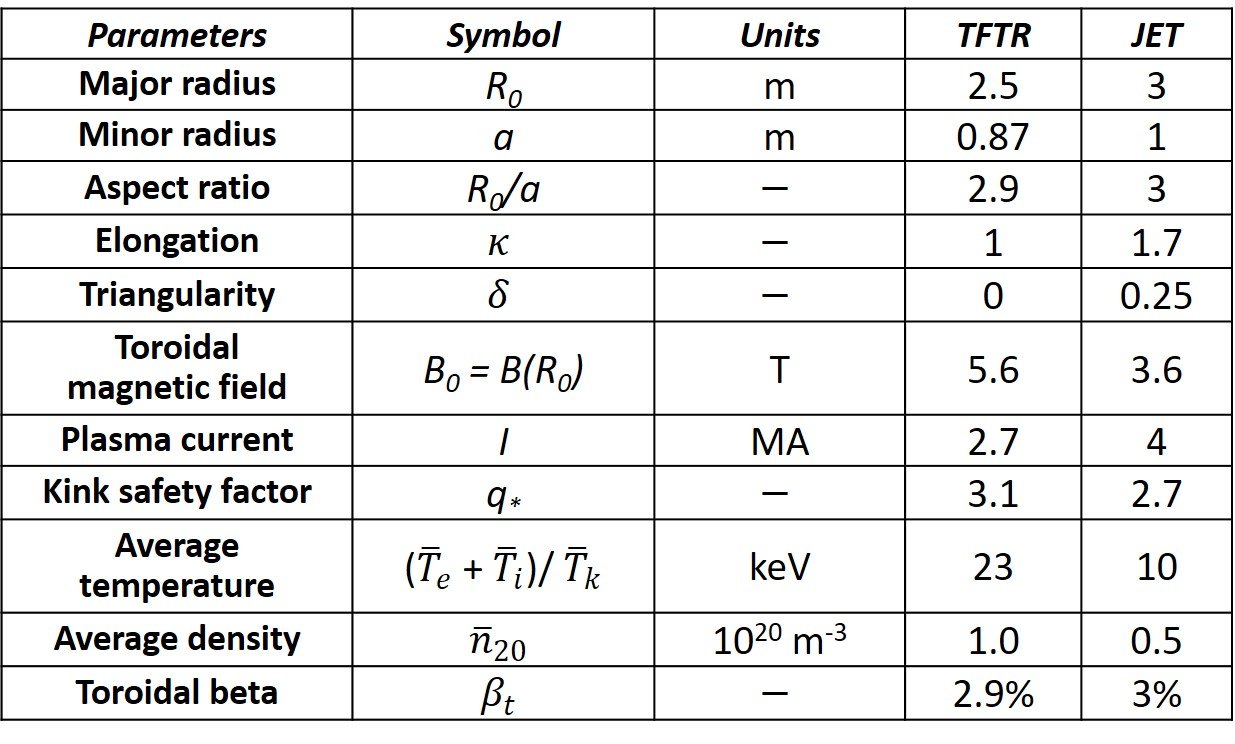
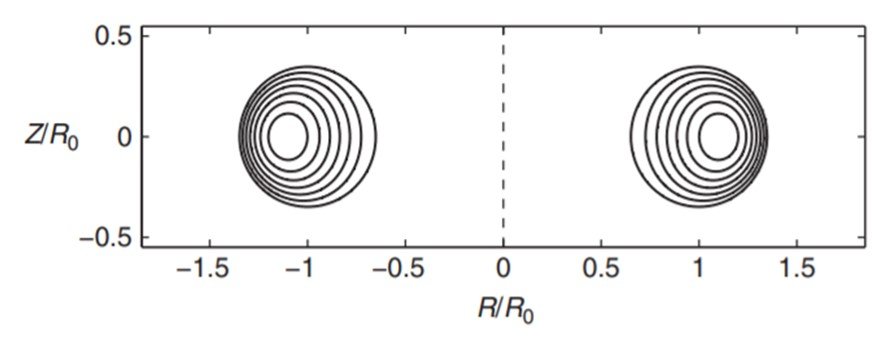
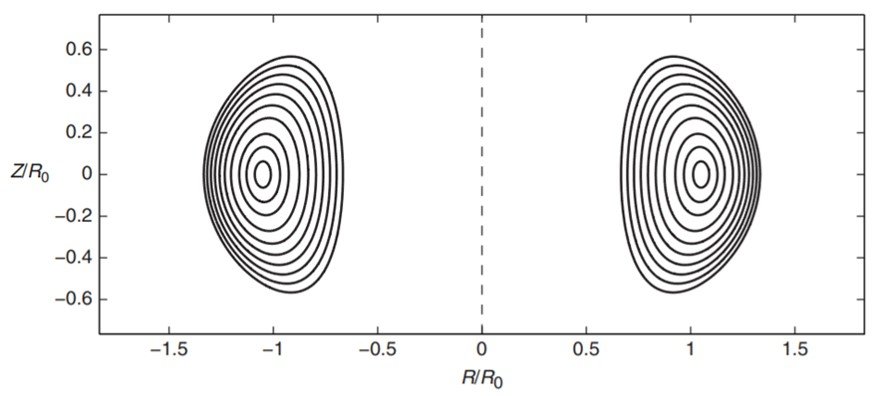
The simplest initial test of the analytic solution procedure is Princeton’s Tokamak Fusion Test Reactor (TFTR), which has a circular cross-section and MHD parameters summarized in Table 1. The analytic solution procedure is applied and the resulting flux surfaces are illustrated in Figure 7. As can be seen, the solution reliably reproduces shifted circular flux surface equilibria.

Figure 7. Exact Solov’ev equilibrium for TFTR.

Another device that can be modelled by the analytical procedure outlined above is the Joint European Torus (JET). Although JET normally operates with a divertor, the analytic procedure assumes that the surface has been smoothed out. JET in fact is a relatively easy test for the equilibrium procedure. Using the values given above, the equilibrium flux surfaces for the solution profiles have been calculated and are illustrated in Figure 8. Observe the elongated “D” shaped plasma and the finite shift of the magnetic axis. The flux surfaces are smooth and nested, showing that the analytic solutions provide a credible representation of high-performance JET equilibria.

Figure 8. Exact Solov’ev equilibrium for JET.

References

• BOYD, T.J.M. and SANDERSON, J.J. (2003). The Physics of Plasmas. Cambridge: Cambridge University Press.

• FREIDBERG, J.P. (2014). Ideal MHD. Cambridge: Cambridge University Press.

• MORSE, E. (2018). Nuclear Fusion. Berlin/Heidelberg: Springer.

• Shafranov, V.D. (1966). Plasma equilibrium in a magnetic field. In: LEONTOVICH, M.A. (Ed.). Reviews of Plasma Physics, Vol. 2. New York: Consultants Bureau.

• STACEY, W.M. (2005). Fusion Plasma Physics. Weinheim: Wiley-VCH.

• WESSON, J. (2004). Tokamaks. Oxford: Clarendon Press.

Tokamaks and the Grad-Shafranov Equation

Subscribe to our Mailing List!

Featured Posts

A Primer on NAND Flash Memories

Solidification Time and Chvorinov’s Rule

Step-Growth Polymerization, the Carothers Equation, and the Flory-Schulz Distribution

More Articles

A Quick Introduction to Convective Mass Transfer Correlations

Aldohexoses: Classification, Haworth Projections, and Chair Conformations

Fields of Study

More

© 2024 Montogue Quiz

Subscribe to
our Mailing List!

Subscribe to our Mailing List!

Subscribe to receive our latest materials in your inbox.

Homework Help

© 2024 Montogue Quiz

Subscribe to our Mailing List!