Aldohexoses: Classification, Haworth Projections, and Chair Conformations

In this article, I provide a brief introduction to the classification and representation of simple aldoses, carbohydrates with an aldehyde group and no more than five or six carbons.

1. Aldoses and ketoses

Simple monosaccharides can be classified as aldoses, when they contain an aldehyde group, or ketoses, when they contain a ketone group. Glucose is an example of aldose, while fructose is an example of ketose.

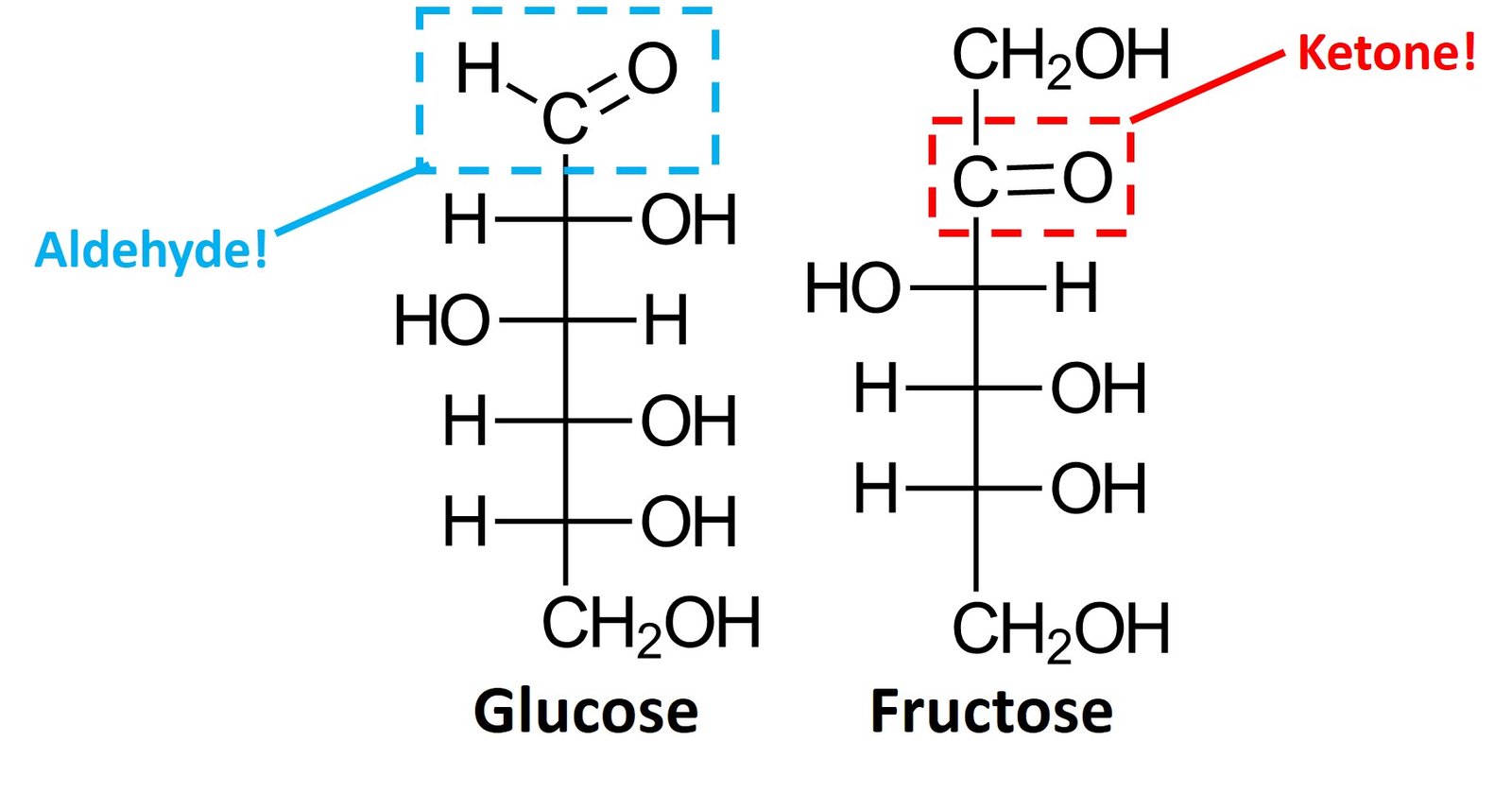
Aldoses and pentoses can be further classified on the basis of their number of carbons, using the typical prefixes tetr- (four carbons), pent– (five carbons), hex- (six carbons), and so forth. Glucose is an aldohexose, while fructose is a ketohexose; the suffix –ose indicates that the molecule is a sugar.

2. D and L sugars

One of the smallest compounds considered to be a carbohydrate is glyceraldehyde, which has a chiral center and therefore can exist as a pair of enantiomers, as shown.

The (+) or D– designations indicate that the enantiomer rotates plane-polarized light in a clockwise fashion (dextrorotatory), while the (-) or L designations are applied to the enantiomer that rotates plane-polarized light in a counterclockwise (levorotatory) sense. The D enantiomer is the only form abundant in nature.

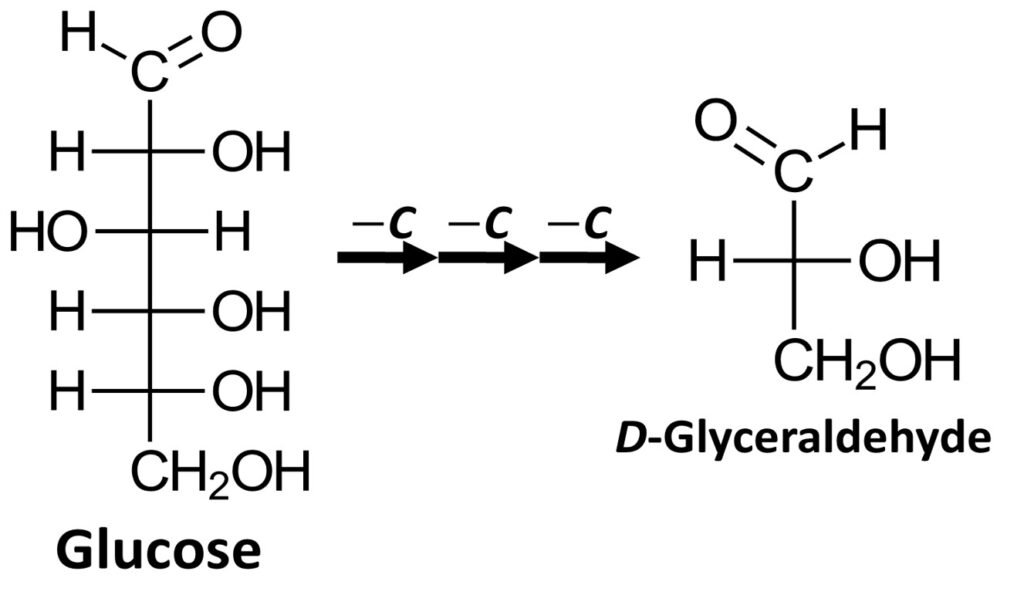
It can be shown that most naturally occurring carbohydrates can be degraded (broken down) to produce D-glyceraldehyde. One example is glucose, which can be stripped of three carbons, from the top to the bottom of the Fischer projection, to yield D-glyceraldehyde. Most naturally occurring monosaccharides can undergo a similar degradation process.

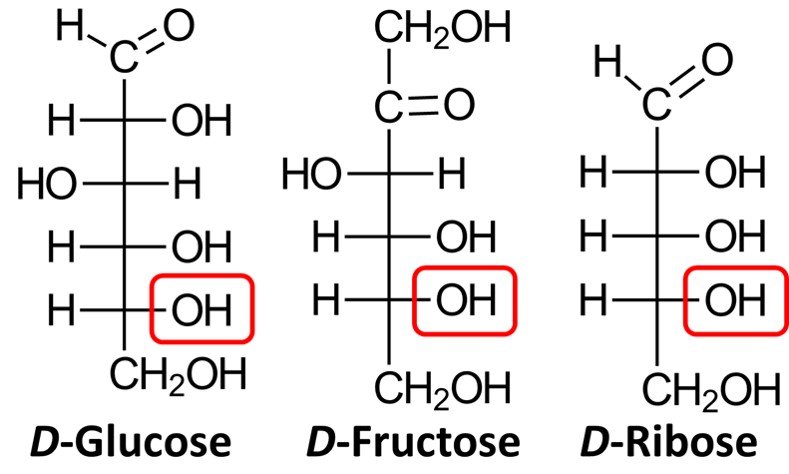
On the other hand, when synthetic sugars are degraded, they produce a mixture of D– and L-glyceraldehyde. In response to this finding, chemists began using the Fischer-Rosanoff convention whereby the prefix D– is attributed to any sugar that degrades to (+)-glyceraldehyde. In accord with this convention, almost all naturally occurring carbohydrates are D-sugars, which means that the chiral center farthest from the carbonyl group will have an OH group pointing to the right in the Fischer projection. Shown below are the Fischer projections of D-glucose, D-fructose, and D-ribose, a common aldopentose. Note how in all three molecules the lowermost chiral center has a hydroxyl group pointing to the right.

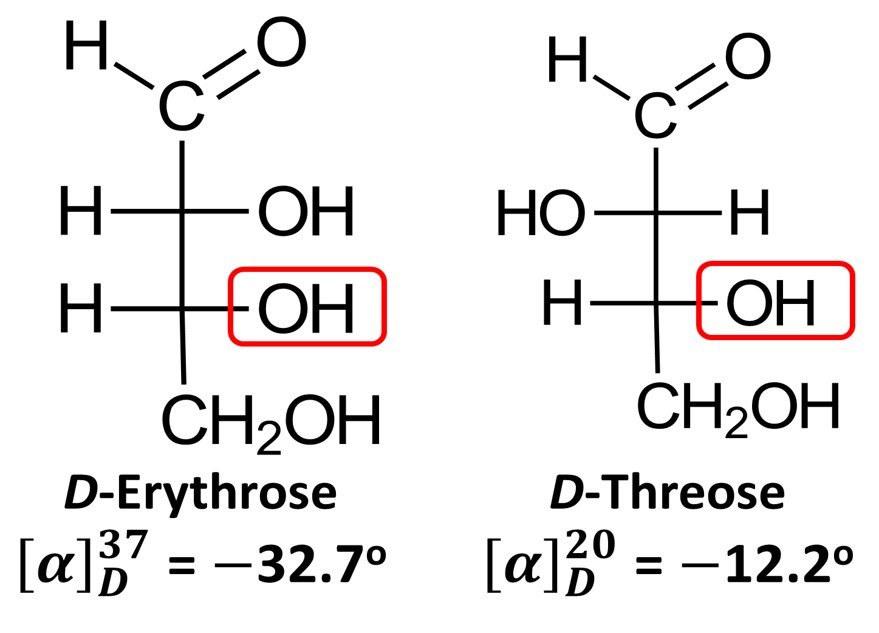
Importantly, while D-glyceraldehyde is dextrorotatory, the D enantiomers of some sugars do not rotate plane-polarized light in a clockwise sense. Examples include D-erythrose, which has specific rotation = –32.7^o (recall that the negative sign denotes counterclockwise rotation), and D-threose, for which = –12.2^o. In view of these exceptions, the D notation in the context of monosaccharides no longer connotes the direction to which the molecule displaces polarized light; rather, it becomes simply an indicator of the fact that the lowermost chiral center has the R configuration, just as it does in (+)-glyceraldehyde. By the same token, a L sugar does not always rotate polarized light counterclockwise; all the L prefix does is indicate that the molecule is the enantiomer of the corresponding R sugar.

3. Simple aldoses

Recall that a given organic molecule has 2ⁿ stereoisomers, where n is the number of chiral centers. Aldotetroses have two chiral centers and hence possess 2² = 4 stereoisomers, or two pairs of enantiomers. Two of the possible aldotetroses are D sugars, while the other two are L sugars. The D isomers are D-erythrose and D-threose, as shown below. The L sugars, L-erythrose and L-threose, are the enantiomers of the D aldotetroses.

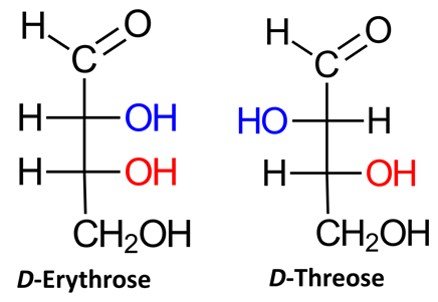
Aldopentoses have three chiral centers, which means that they have 2³ = 8 stereoisomers, or four pairs of enantiomers. Four of the possible aldopentoses are D sugars, while the other four are L sugars. Shown below are the D sugars.

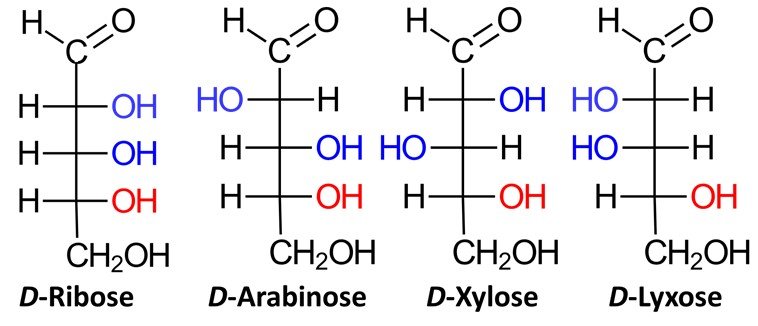
Aldohexoses have four chiral centers, giving rise to 2⁴ = 16 possible stereoisomers, or eight pairs of enantiomers. The eight possible D sugars are D-allose, D-altrose, D-glucose, D-mannose, D-gulose, D-idose, D-galactose, and D-talose.

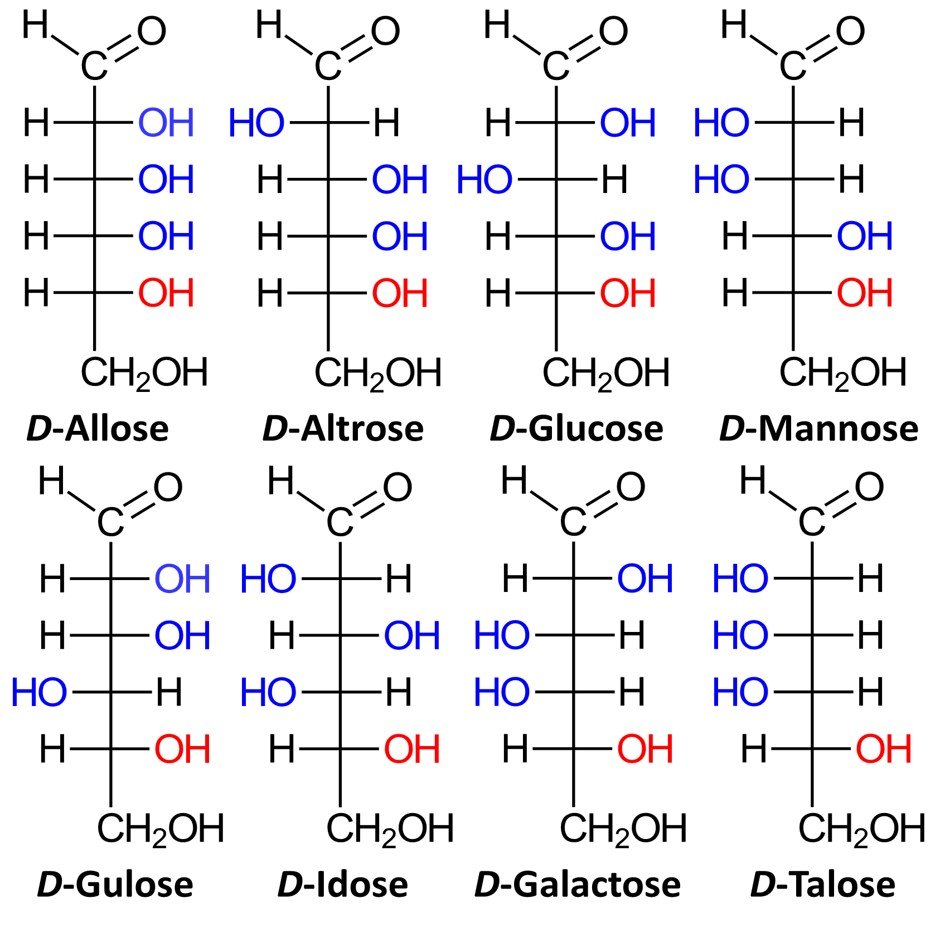
The family of basic D aldoses, starting with D-glyceraldehyde, is summarized below.

The four aldopentoses can be memorized by the simple mnemonic “ribs are extra lean.” Louis Fieser of Harvard University, quoted in McMurry (2008), suggests a simple procedure to remember the names and structures of the D-aldohexoses:

Step 1. Set up eight Fischer projections with the -CHO group on top and the -CH₂OH group at the bottom.

Step 2. At C5, place all eight –OH groups to the right; these are, after all, D sugars.

Step 3. At C4, alternate four –OH groups to the right and four to the left.

Step 4. At C3, alternate two –OH groups to the right, two to the left, two to the right, and two to the left.

Step 5. At C2, alternate –OH groups right, left, right, left, and so on.

Step 6. Name the eight isomers using the mnemonic “all altruists gladly make gum in gallon tanks.”

4. Pyranose form of aldohexoses

A compound containing both an OH group and an aldehyde group can undergo an intramolecular transformation to form a cyclic hemiacetal. Such conversions occur in carbohydrates such as glucose. A Haworth projection can be used to indicate the configuration at each chiral center.

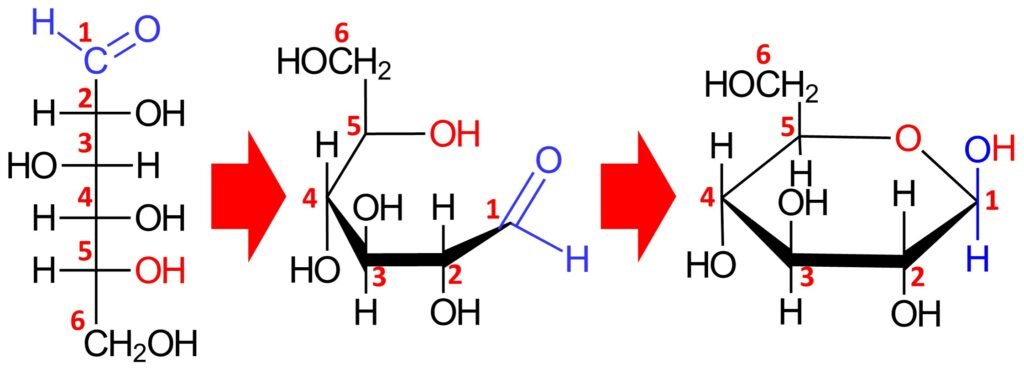
In the cyclic form, the ring is called a pyranose ring, named after pyran, a simple compound that possesses a six-membered ring with an oxygen atom incorporated in the ring. The cyclic hemiacetal form of a monosaccharide is defined by a prefix that refers to the original sugar (e.g., gluco- for glucose or manno- for mannose) plus the suffix –pyranose. Accordingly, the cyclic structure above is called glucopyranose.

Equilibrium favors the formation of the cyclic hemiacetal form; indeed, D-glucose exists almost exclusively in the cyclic hemiacetal form, and only a trace amount of the open-chain form is present at equilibrium.

When D-glucose is closed into a cyclic hemiacetal, two different stereoisomers of D-glucopyranose can be formed. The aldehydic carbon (C1) becomes a chiral center, and both configurations for that new carbon are possible. The C1 position is called the anomeric carbon, and the stereoisomers are called anomers. The two anomers are identified by the prefixes  and . In the  anomer, the hydroxyl group at the anomeric carbon is trans to the CH₂OH group, while in the  anomer the hydroxyl group is cis to the CH₂OH group. Shown below are -D-glucopyranose and –D-glucopyranose.

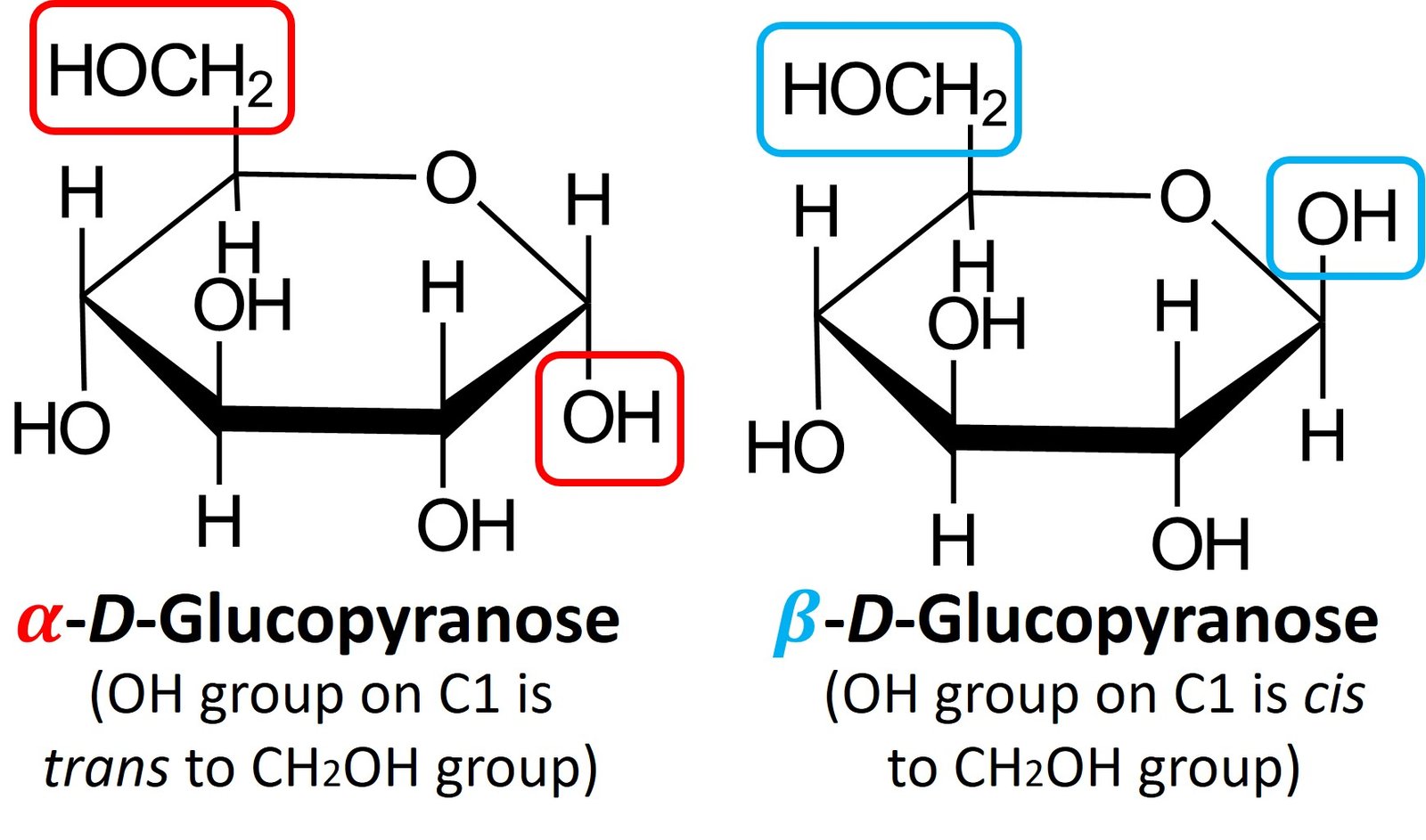
Both anomers of D-glucopyranose can be crystallized and purified. Pure –D-glucopyranose has a melting point of 146^oC and a specific rotation, , of +112.2^o; pure –D-glucopyranose has a melting point of 148^oC to 155^oC and a specific rotation of +18.7^o. When a sample of either pure anomer is dissolved in water, however, the optical rotation slowly changes and ultimately reaches a constant value of +52.6^o. That is, the specific rotation of the -anomer solution decreases from +112.2 to +52.6, and the specific rotation of the -anomer solution increases from +18.7 to +52.6. Called mutarotation, this change in optical rotation is due to the slow conversion of the pure anomers into a 37:63 equilibrium mixture.

5. Drawing Haworth projections of aldohexoses

Let’s work out how to draw the Haworth projection of a sugar’s hemiacetal form. We’ve used glucose a lot already, so let’s consider a different molecule; I’ve chosen –D-mannopyranose. For the Fischer projection of D-mannose, refer to the family of aldoses given in section 3. The first step is to draw a hexagonal ring with the oxygen atom on the back right position:

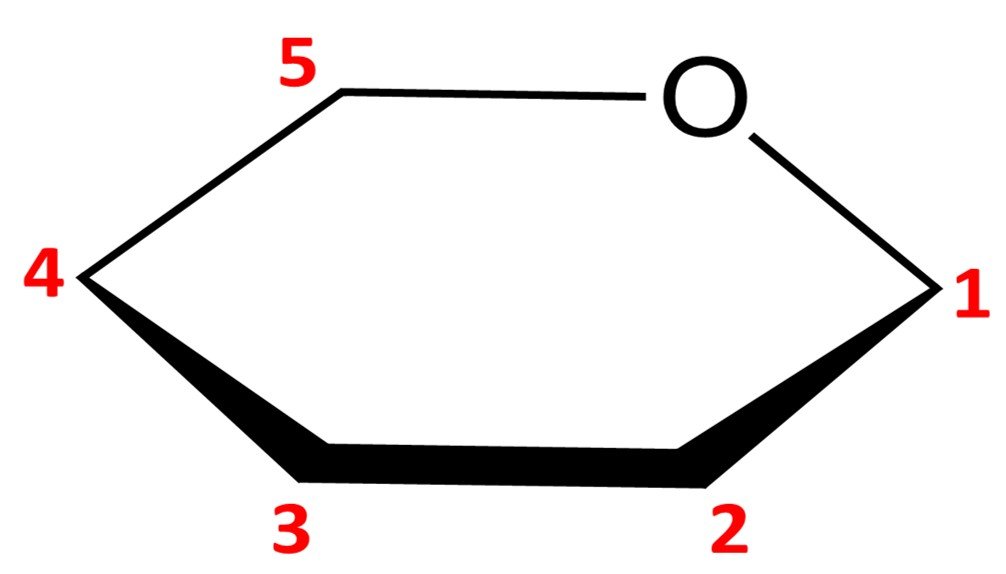
Notice that this leaves us with only five vertices to place carbon atoms, but aldohexoses have six carbons. The solution is simple: the carbon in the C5 position is endowed with a CH₂OH group instead of a simple hydroxyl. The orientation of the CH₂OH group in the Haworth projection is dictated by whether the sugar is a D or L isomer: a D isomer such as –D-mannopyranose will have the CH₂OH group pointing up, while a L isomer will have it pointing down.

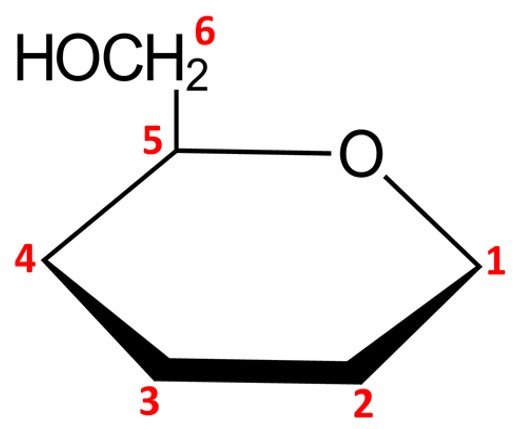
We can then proceed to adjust the remaining carbons in the pyranose ring. As explained in the previous section, the configuration at C1, the anomeric carbon, stems from the name of the pyranose ring form: an  anomer should have its hydroxyl pointing down (that is, trans to the CH₂OH group attached to the C5 carbon), while a  anomer should have its hydroxyl pointing up (cis to the CH₂OH group). Accordingly, –D-mannopyranose should look as follows:

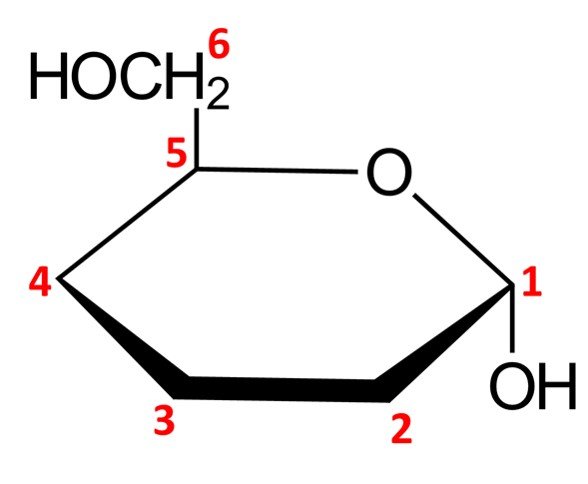
The remaining chiral centers, C2, C3, and C4, are quite straightforward to draw. Any OH groups that appear on the right side of the Fischer projection when drawn in open-chain form will be pointing down in the Haworth projection of the cyclic form, while OH groups that appear on the left side of the Fischer projection will be placed pointing up in the Haworth projection. For –D-mannopyranose, we have the following configuration:

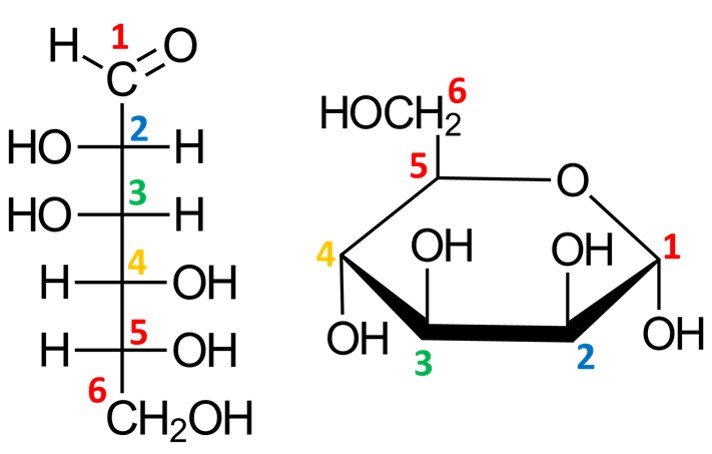
This completes the Haworth projection of the molecule at hand.

6. Drawing chair conformations of aldohexoses

While Haworth projections are useful for showing configurations, they are not effective for communicating the conformation of a compound. Chair conformations are much more valuable for this purpose. Drawing the chair conformation of a pyranose ring is quite easy.

Take, for instance, –D-mannopyranose. The first step is to place the oxygen in the upper, rear-right position of the chair skeleton, as shown.

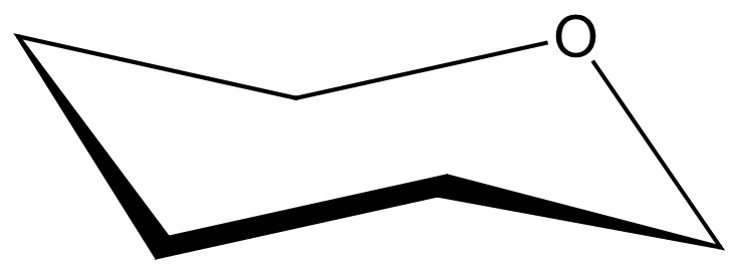
Next, we are left with five vertices to represent the pyranose carbons, beginning at C1, which is placed adjacent to the oxygen atom in a clockwise sense. As in the Haworth projection, carbon C6 will appear in form of a CH₂OH group attached to the C5 carbon.

Once the carbons have been numbered, the hydroxyls must be drawn. Orientations are preserved: any OH groups pointing up in the Haworth projection will appear in upper positions when drawn in the chair conformation, while OH groups pointing down in the Haworth projection will be in lower positions when transferred to the chair conformation. For –D-mannopyranose, the resulting conformation should look as follows:

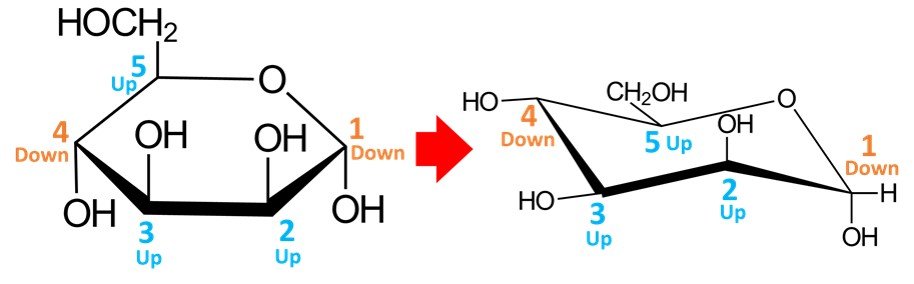
In a quick analysis of this chair conformation, notice that there are two hydroxyls in axial positions and two in equatorial positions. The CH₂OH group is in an equatorial position.

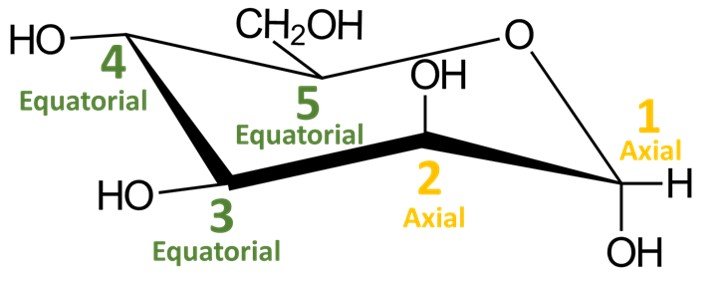
Recall that a cyclic compound can adopt two chair conformations. The other conformation would be obtained by performing a ring flip, that is, by switching all equatorial substituents to axial positions and vice versa; try doing it yourself. You should obtain the following structure:

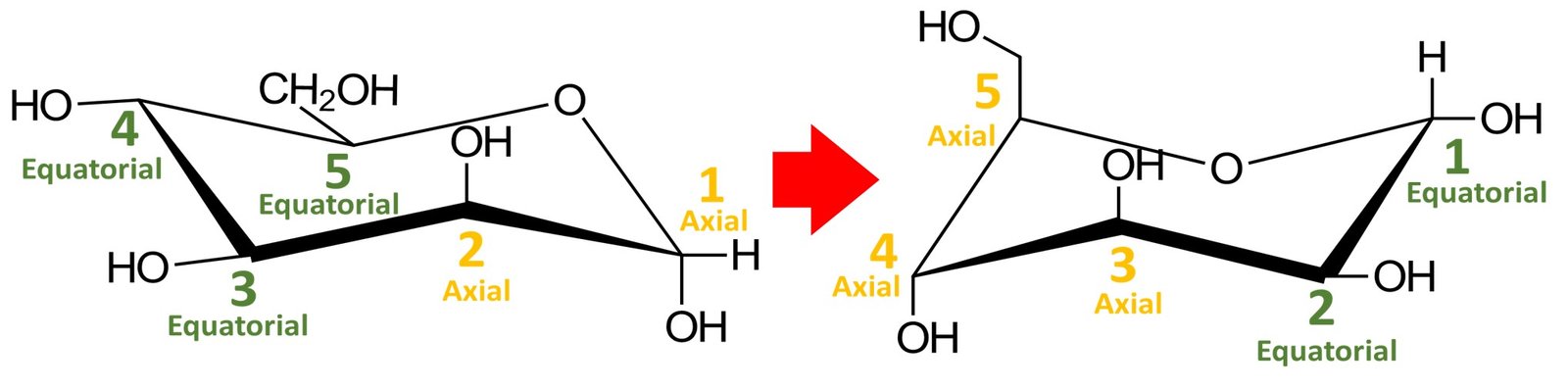
Which chair conformation, left or right, is the most stable? The most stable chair conformation is the one in which the largest groups occupy equatorial positions. In aldohexoses, the CH₂OH group is the bulkiest substituent, so the most stable chair conformation will be the one in which this group occupies an equatorial position. This is the case for the chair conformation shown to the left.

7. Extra exercise

We’ve seen how to convert Fischer projections to Haworth projections and how to convert Haworth projections to chair conformations. A last logical task would be to draw Fischer projections from chair conformations. As an example, consider the following molecule.

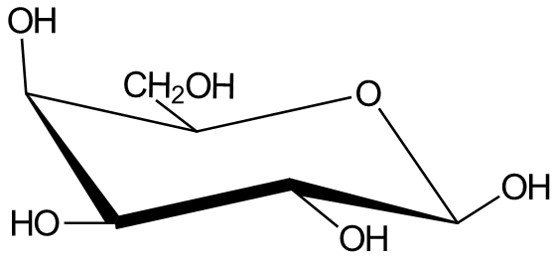
We begin by numbering carbons C1 to C6, starting at the carbon adjacent to the oxygen atom in a clockwise sense.

Carbon C1, the anomeric carbon, will become an aldehyde group in the open-chain form. The OH group at C5 must be pointing to the right in the Fischer projection, because it is pointing “up” in the chair conformation; in other words, this is a D-sugar. It remains to establish the position of the hydroxyls in carbons C2, C3 and C4; to do so, simply note that carbons that point “up” in the chair conformation will appear pointing to the left in the Fischer projection, while carbons pointing “down” in the chair conformation will appear pointing to the right when drawn in open form. In short, bear in mind that the rule for the orientation of the OH group connected to carbon C5 is different from the rule for the orientation of the hydroxyls connected to carbons C2, C3 and C4.

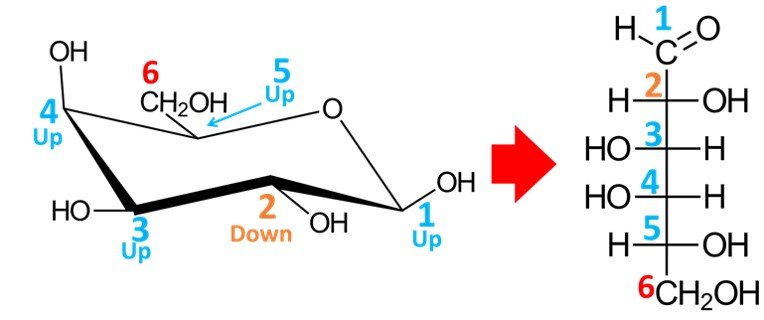
As shown above, the resulting aldohexose is D-galactose.

Go further

Further problems on the organic chemistry of sugars can be found in our free problem set on carbohydrates, amino acids and lipids, which you can find here. Biomolecules are also covered in our free quiz Cell and Molecular Biology.

References

• KLEIN, D. (2017). Organic Chemistry. 3rd edition. Hoboken: John Wiley and Sons.

• MCMURRY, J. (2008). Organic Chemistry. 7th edition. Toronto: Thomson.