Cruise Flight Performance of Piston-Prop Aircraft

This article is a complement to our PDF on aircraft performance. That problem set covered cruise flight of turbojet planes, not piston-prop craft. The latter are considered in the present article.

Range and endurance of piston-prop aircraft

The range of constant altitude-constant lift coefficient cruise flight for a turboprop plane is given by

$\displaystyle {{x}_{{h-{{C}_{L}}}}}=\frac{{k{{\eta }_{P}}E}}{{\hat{c}}}\ln \left( {\frac{1}{{1-\zeta }}} \right)\,\,\,(\text{I})$

Here, $\displaystyle {{\eta }_{p}}$ is propeller efficiency, E is aerodynamic efficiency, $\displaystyle \hat{c}$ is the power-specific fuel consumption (PSFC), $\displaystyle \zeta$ is the fuel weight fraction, and k is a constant. The value of k depends on the system of units used to represent brake power. If the engine power is prescribed in horsepower, k = 550 ft-lb/s-hp. If the engine power is in kilowatts, the value of k = 1000 W/kW. Lastly, if brake power is given in a standard system of units, either foot/pound/second (FPS) or SI, the value of k = 1.

The range of constant airspeed-constant lift coefficient flight is the same as that of a constant $\displaystyle h-{{C}_{L}}$ flight, namely,

$\displaystyle {{x}_{{V-{{C}_{L}}}}}=\frac{{k{{\eta }_{P}}E}}{{\hat{c}}}\ln \left( {\frac{1}{{1-\zeta }}} \right)\,\,\,(\text{II})$

The range of a constant altitude-constant airspeed flight is given by

$\displaystyle {{x}_{{h-V}}}=\frac{{2k{{\eta }_{p}}{{E}_{m}}}}{{\hat{c}}}{{\tan }^{{-1}}}\left[ {\frac{{{{E}_{1}}\zeta }}{{2{{E}_{m}}\left( {1-K{{E}_{1}}{{C}_{{L,1}}}\zeta } \right)}}} \right]\,\,\,(\text{III})$

In addition to the familar variables, here we have the induced drag correction factor K and the maximum aerodynamic efficiency $\displaystyle {{E}_{m}}$ = 1/2 $\displaystyle \sqrt{{K{{C}_{{D,0}}}}}$ . Subscript 1 denotes values considered at the start of cruise.

The endurance of constant altitude-constant lift coefficient flight is given by

$\displaystyle {{t}_{{h-{{C}_{L}}}}}=\frac{{2k{{\eta }_{p}}E}}{{\hat{c}{{V}_{1}}}}\left( {\frac{1}{{\sqrt{{1-\zeta }}}}-1} \right)\,\,\,(\text{IV})$

The endurance of constant airspeed-constant lift coefficient flight is obtained by dividing equation (II) by the airspeed V, giving

$\displaystyle {{t}_{{V-{{C}_{L}}}}}=\frac{{{{x}_{{V-{{C}_{L}}}}}}}{V}\,\,\,(\text{V})$

In a similar manner, the endurance of constant altitude-constant airspeed flight is obtained by dividing equation (III) by the airspeed, that is,

$\displaystyle {{t}_{{h-V}}}=\frac{{{{x}_{{h-V}}}}}{V}\,\,\,(\text{VI})$

Application to an aircraft – part 1

Consider an aircraft of weight 7500 N, wing area 11.5 m², and drag coefficient given by $\displaystyle {{C}_{D}}$ = 0.031 + 0.143 $\displaystyle C_{L}^{2}$ . It is flying at an altiitude of 4 km with a piston-prop engine whose propeller efficiency is 0.82 and whose power specific fuel consumption is $\displaystyle 5\times {{10}^{{-7}}}$ N/s/W. The cruise-fuel weight fraction of the aircraft is 0.11. If the airspeed of the aircraft is 290 km/h, find the range and endurance during cruise in the cases of constant $\displaystyle h-{{C}_{L}}$ , constant $\displaystyle V-{{C}_{L}}$ , and constant $\displaystyle h-V$ flights.

The wing loading is W/S = 7500/11.5 = 652 N/m². The airspeed is converted as V = 290/3.6 = 80.6 m/s. The density of air at sea level is $\displaystyle {{\rho }_{{SSL}}}$ = 1.225 kg/m³. For an altitude of 4000 m, we take the density ratio $\displaystyle \sigma$ = 0.6689 (see, e.g., The Engineering Toolbox). The lift coefficient of the aircraft at the start of cruise is given by

$\displaystyle {{C}_{L}}=\frac{{2\left( {W/S} \right)}}{{{{\rho }_{{SSL}}}\sigma {{V}^{2}}}}=\frac{{2\times 652}}{{1.225\times 0.6689\times {{{80.6}}^{2}}}}=0.245$

The drag coefficient is given by the drag polar as

$\displaystyle {{C}_{D}}=0.031+0.143\times {{0.245}^{2}}=0.0396$

The aerodynamic efficiency at the start of cruise is $\displaystyle E$ = $\displaystyle {{C}_{L}}$ / $\displaystyle {{C}_{D}}$ = 0.245/0.0396 = 6.19. The value of k for SI units is 1.0. The range for constant $\displaystyle h-{{C}_{L}}$ flight is given by equation (I),

$\displaystyle {{x}_{{h-{{C}_{L}}}}}=\frac{{k{{\eta }_{P}}E}}{{\hat{c}}}\ln \left( {\frac{1}{{1-\zeta }}} \right)$

$\displaystyle {{x}_{{h-{{C}_{L}}}}}=\frac{{1.0\times 0.82\times 6.19}}{{5\times {{{10}}^{{-7}}}}}\ln \left( {\frac{1}{{1-0.11}}} \right)=1.18\times {{10}^{6}}\,\text{m}=1180\,\,\text{km}\leftarrow$

The corresponding endurance is given by equation (IV),

$\displaystyle {{t}_{{h-{{C}_{L}}}}}=\frac{{2k{{\eta }_{p}}E}}{{\hat{c}{{V}_{1}}}}\left( {\frac{1}{{\sqrt{{1-\zeta }}}}-1} \right)$

$\displaystyle {{t}_{{h-{{C}_{L}}}}}=\frac{{2\times 1.0\times 0.82\times 6.19}}{{\left( {5\times {{{10}}^{{-7}}}} \right)\times 80.6}}\times \left( {\frac{1}{{\sqrt{{1-0.11}}}}-1} \right)=15,100\,\,\text{s}=4.19\,\text{h}\leftarrow$

The range for a constant $\displaystyle V-{{C}_{L}}$ flight is the same as that for constant $\displaystyle h-{{C}_{L}}$ flight; that is,

$\displaystyle {{x}_{{V-{{C}_{L}}}}}={{x}_{{h-{{C}_{L}}}}}=1180\,\,\text{km}\leftarrow$

The corresponding endurance is

$\displaystyle {{t}_{{V-{{C}_{L}}}}}=\frac{{1.18\times {{{10}}^{6}}}}{{80.6}}=14,600\,\,\text{s}=4.06\,\,\text{h}\leftarrow$

The range of constant $\displaystyle h-V$ flight follows from equation (III). Before proceeding, we require the maximum aerodynamic efficiency 1/ $\displaystyle 2\sqrt{{0.031\times 0.143}}$ = 7.51. Accordingly,

$\displaystyle {{x}_{{h-V}}}=\frac{{2k{{\eta }_{p}}{{E}_{m}}}}{{\hat{c}}}{{\tan }^{{-1}}}\left[ {\frac{{{{E}_{1}}\zeta }}{{2{{E}_{m}}\left( {1-K{{E}_{1}}{{C}_{{L,1}}}\zeta } \right)}}} \right]$

$\displaystyle {{x}_{{h-V}}}=\frac{{2\times 1.0\times 0.82\times 7.51}}{{5.0\times {{{10}}^{{-7}}}}}{{\tan }^{{-1}}}\left[ {\frac{{6.19\times 0.11}}{{2\times 7.51\times \left( {1-0.143\times 6.19\times 0.245\times 0.11} \right)}}} \right]=1.14\times {{10}^{6}}\,\text{m}=1140\,\,\text{km}\leftarrow$

The corresponding endurance is straightforwardly obtained as

$\displaystyle {{t}_{{h-V}}}=\frac{{{{x}_{{h-V}}}}}{V}=\frac{{1.14\times {{{10}}^{6}}}}{{80.6}}=14,100\,\,\text{s}=3.93\,\,\text{h}$

The results are summarized in the following table.

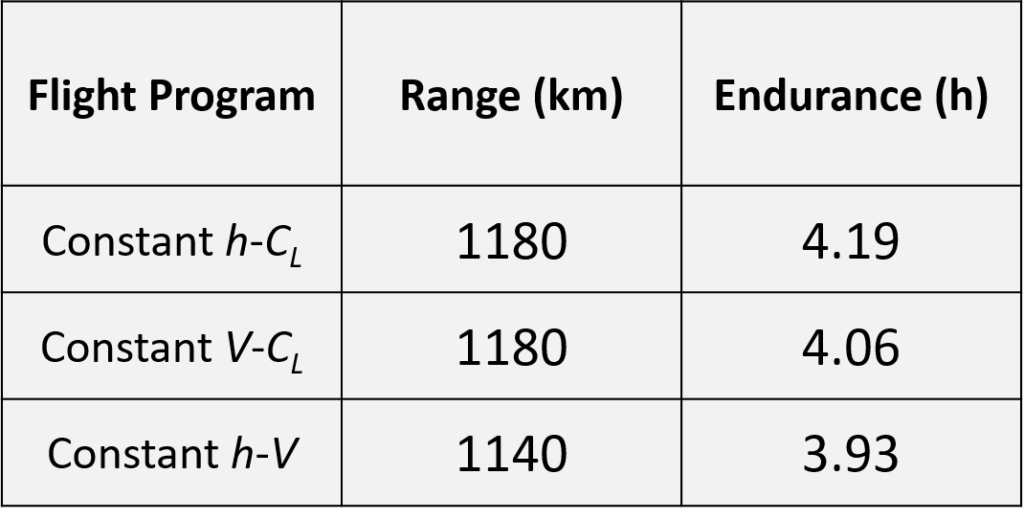
Maximum-range cruise flight of piston-prop aircraft

The maximum-range airspeed of a piston-prop craft in constant $\displaystyle V-{{C}_{L}}$ flight or a constant $\displaystyle h-{{C}_{L}}$ flight can be shown to be

$\displaystyle {{V}_{{MR,V-{{C}_{L}}}}}={{V}_{{MR,h-{{C}_{L}}}}}={{\left[ {\frac{{2\left( {{W}/{S}\;} \right)}}{{{{\rho }_{{SSL}}}\sigma }}} \right]}^{{{1}/{2}\;}}}{{\left( {\frac{K}{{{{C}_{{D,0}}}}}} \right)}^{{{1}/{4}\;}}}\,\,(\text{VII})$

The maximum range for a constant $\displaystyle V-{{C}_{L}}$ or a constant $\displaystyle h-{{C}_{L}}$ flight is

$\displaystyle {{x}_{{MR,V-{{C}_{L}}}}}={{x}_{{MR,h-{{C}_{L}}}}}=\frac{{k{{\eta }_{p}}{{E}_{m}}}}{{\hat{c}}}\ln \left( {\frac{1}{{1-\zeta }}} \right)\,\,\,(\text{VIII})$

which is identical to equation (II), with the exception that the aerodynamic efficiency $\displaystyle E$ has been replaced with the maximum value $\displaystyle {{E}_{m}}$ .

The maximum-range airspeed for constant $\displaystyle h-V$ flight is given by

$\displaystyle {{V}_{{MR,h-V}}}={{\left[ {\frac{{2\left( {{{{{W}_{1}}}}/{S}\;} \right)}}{{{{\rho }_{{SSL}}}\sigma }}} \right]}^{{{1}/{2}\;}}}{{\left[ {\frac{{K\left( {1-{{\zeta }^{*}}} \right)}}{{{{C}_{{D,0}}}}}} \right]}^{{{1}/{4}\;}}}\,\,\,(\text{IX})$

Lastly, the maximum range for constant $\displaystyle h-V$ flight is expressed as

$\displaystyle {{x}_{{MR,h-V}}}=\frac{{2k{{\eta }_{p}}{{E}_{m}}}}{{\hat{c}}}{{\tan }^{{-1}}}\left( {\frac{\zeta }{{2\sqrt{{1-\zeta }}}}} \right)\,\,\,(\text{X})$

Application to an aircraft – part 2

Reconsider the previous numerical example. We are now interested in the maximum-range airspeed, the maximum range, and the endurance for constant $\displaystyle V-{{C}_{L}}$ and constant $\displaystyle h-V$ flights.

The maximum-range airspeed for constant $\displaystyle V-{{C}_{L}}$ flight is given by equation (VII),

$\displaystyle {{V}_{{MR,V-{{C}_{L}}}}}={{\left[ {\frac{{2\left( {{W}/{S}\;} \right)}}{{{{\rho }_{{SSL}}}\sigma }}} \right]}^{{{1}/{2}\;}}}{{\left( {\frac{K}{{{{C}_{{D,0}}}}}} \right)}^{{{1}/{4}\;}}}$

$\displaystyle {{V}_{{MR,V-{{C}_{L}}}}}={{\left( {\frac{{2\times 652}}{{1.225\times 0.6689}}} \right)}^{{{1}/{2}\;}}}\times {{\left( {\frac{{0.143}}{{0.031}}} \right)}^{{{1}/{4}\;}}}=58.5\,\,{\text{m}}/{\text{s}}\;\leftarrow$

or, equivalently, 211 km/h. The maximum range for constant $\displaystyle V-{{C}_{L}}$ flight is calculated with equation (VIII),

$\displaystyle {{x}_{{MR,V-{{C}_{L}}}}}=\frac{{k{{\eta }_{P}}{{E}_{m}}}}{{\hat{c}}}\ln \left( {\frac{1}{{1-\zeta }}} \right)$

$\displaystyle {{x}_{{MR,V-{{C}_{L}}}}}=\frac{{1.0\times 0.82\times 7.51}}{{5.0\times {{{10}}^{{-7}}}}}\ln \left( {\frac{1}{{1-0.11}}} \right)=1.44\times {{10}^{6}}\,\text{m}=1440\,\,\text{km}$

The corresponding endurance is

$\displaystyle {{t}_{{MR,V-{{C}_{L}}}}}=\frac{{{{x}_{{MR,V-{{C}_{L}}}}}}}{{{{V}_{{MR,V-{{C}_{L}}}}}}}=\frac{{1.44\times {{{10}}^{6}}}}{{58.5}}=24,600\,\,\text{s}=6.83\,\,\text{h}$

Next, the maximum-range airspeed for constant $\displaystyle h-V$ flight is computed using equation (IX),

$\displaystyle {{V}_{{MR,h-V}}}={{\left( {\frac{{2\times 652}}{{1.225\times 0.6689}}} \right)}^{{{1}/{2}\;}}}{{\left[ {\frac{{0.143\times \left( {1-0.11} \right)}}{{0.031}}} \right]}^{{{1}/{4}\;}}}=56.8\,\,{\text{m}}/{\text{s}}\;$

or, equivalently, 204 km/h. The maximum range for this flight program follows from equation (X),

$\displaystyle {{x}_{{MR,h-V}}}=\frac{{2k{{\eta }_{p}}{{E}_{m}}}}{{\hat{c}}}{{\tan }^{{-1}}}\left( {\frac{\zeta }{{2\sqrt{{1-\zeta }}}}} \right)$

$\displaystyle {{x}_{{MR;h-V}}}=\frac{{2\times 1.0\times 0.82\times 7.51}}{{5.0\times {{{10}}^{{-7}}}}}{{\tan }^{{-1}}}\left( {\frac{{0.11}}{{2\sqrt{{1-0.11}}}}} \right)=1.43\times {{10}^{6}}\,\,\text{m}=1.430\,\,\text{km}\leftarrow$

The corresponding endurance is

$\displaystyle {{t}_{{MR,h-V}}}=\frac{{{{x}_{{MR,h-V}}}}}{{{{V}_{{MR,h-V}}}}}=\frac{{1.43\times {{{10}}^{6}}}}{{56.8}}=25,100\,\,\text{s}=6.97\,\,\text{h}$

The maximum-range airspeed, maximum range, and the endurance for the two flight programs have been established. Our results are summarized below.

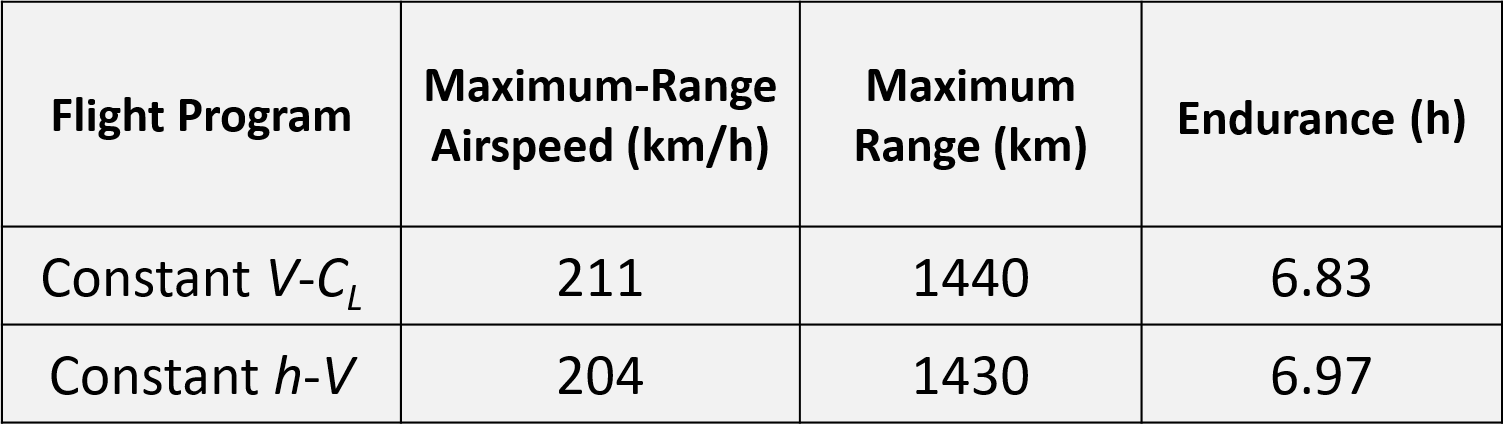
Go further

As mentioned above, Montogue offers a free set of problems for students of aircraft performance, which you can find here. You may also be interested in our problem sets on aircraft propulsion and airfoil theory. Check them out!

References

• HALE, F. (1984). Aircraft Performance, Selection, and Design. Hoboken: John Wiley and Sons.

• OJHA, S. (1995). Flight Performance of Aircraft. Washington: AIAA.

Cruise Flight Performance of Piston-Prop Aircraft

Subscribe to our Mailing List!

Featured Posts

A Primer on NAND Flash Memories

Solidification Time and Chvorinov’s Rule

Step-Growth Polymerization, the Carothers Equation, and the Flory-Schulz Distribution

More Articles

Oscillatory Flow in a Rigid Circular Tube

Vertical-Axis Wind Turbines

Fields of Study

More

© 2024 Montogue Quiz

Subscribe to
our Mailing List!

Subscribe to our Mailing List!

Subscribe to receive our latest materials in your inbox.

Homework Help

© 2024 Montogue Quiz

Subscribe to our Mailing List!