In mining, the energy consumed in comminution operations is often higher than in other operations, such as screening, beneficiation, dewatering and conveying. Accordingly, much attention is paid to this aspect of the mineral processing sequence.
Comminution models fall into three categories: empirical, phenomenological, and fundamental. Under the empirical umbrella are energy-based methods, which are some of the oldest approaches to analysis of ore size reduction. Energy-based models assume a relationship between the energy input of the comminution device and the resultant effective particle size of the product. The energy input is for net power, that is, after correcting for motor efficiency and drive train mechanical losses; typically, energy is measured as kWh/t or joules, depending on the model. Energy-based methods date back to the mid/late 19th century. The pioneering effort came in 1867, when the Austrian mineral scientist Peter R. von Rittinger proposed the first of the three models that came to be known as the “laws of comminution.” The second such model was proposed by Friedrich Kick, also an Austrian-born investigator, in 1885. The third result is due to Fred C. Bond, an outstanding American mining engineer who first published the results of his immense empirical work in 1952. All three equations developed by these authors can be gleaned in the same basic differential equation
where E is the net energy required per unit weight (specific energy), x is an index describing the size distribution, n is an exponent indicating the order of the process, and C is a constant related to material properties and the units chosen to balance the equation. Applying integrals to the equation above, we can write
where F and P are some measure of feed and product size, usually diameters. Letting n = 2, 1, or 1.5 yields the three comminution laws due to von Rittinger, Kick, and Bond, respectively.
As mentioned above, the oldest theory is due to von Rittinger, who stated that the energy consumed is proportional to the area of new surface produced. The surface area of a known weight of particles of uniform diameter is inversely proportional to the diameter, hence von Rittinger’s law can be stated as
which is the result of the integral introduced above when n = 2. KVR is a constant associated with the resistance of the material to comminution.
The second comminution theory is due to Kick, who suggested that the energy required is proportional to the reduction in volume of the particles. Substituting n = 1 in the general equation and carrying out the integration gives one form of the Kick equation,
where F/P is the reduction ratio. One immediate implication of Kick’s theory is that energy requirement depends only on the reduction ratio, and not on the original size of the particles. This is seldom true in situations of mining interest.
The third theory of comminution was published by Bond in the 1950s. Bond states that the total work useful in breakage that has been applied to a given weight of homogeneous broken material is inversely proportional to the square root of the average size of the product particles, directly proportional to the length of crack tips formed, and directly proportional to the square root of new surface created. In mathematical terms, we may write
where W is the energy input in kilowatt hours per metric ton (or per short ton in Bond’s initial publications), P is the diameter of product particles, F is the diameter of feed particles, and KB is a constant. In order to apply this equation, constant KB must be evaluated. To do so, we appeal to another parameter introduced by Bond, the so-called work index Wi, which is the gross rate in kWhr/short ton of feed necessary to reduce a very large feed to such a size that 80% of product passes the 100 microns screen. Substituting P = 100 
![\displaystyle W={{W}_{i}}={{K}_{B}}\left[ {\frac{1}{{\sqrt{{100}}}}-\frac{1}{{\sqrt{\infty }}}} \right]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+W%3D%7B%7BW%7D_%7Bi%7D%7D%3D%7B%7BK%7D_%7BB%7D%7D%5Cleft%5B+%7B%5Cfrac%7B1%7D%7B%7B%5Csqrt%7B%7B100%7D%7D%7D%7D-%5Cfrac%7B1%7D%7B%7B%5Csqrt%7B%5Cinfty+%7D%7D%7D%7D+%5Cright%5D&bg=ffffff&fg=000&s=1&c=20201002)
so that the Bond equation can be restated as
Values of the Bond work index for some ores and minerals are listed in Table 1.
Table 1. Values of the Bond work index for common ores and minerals
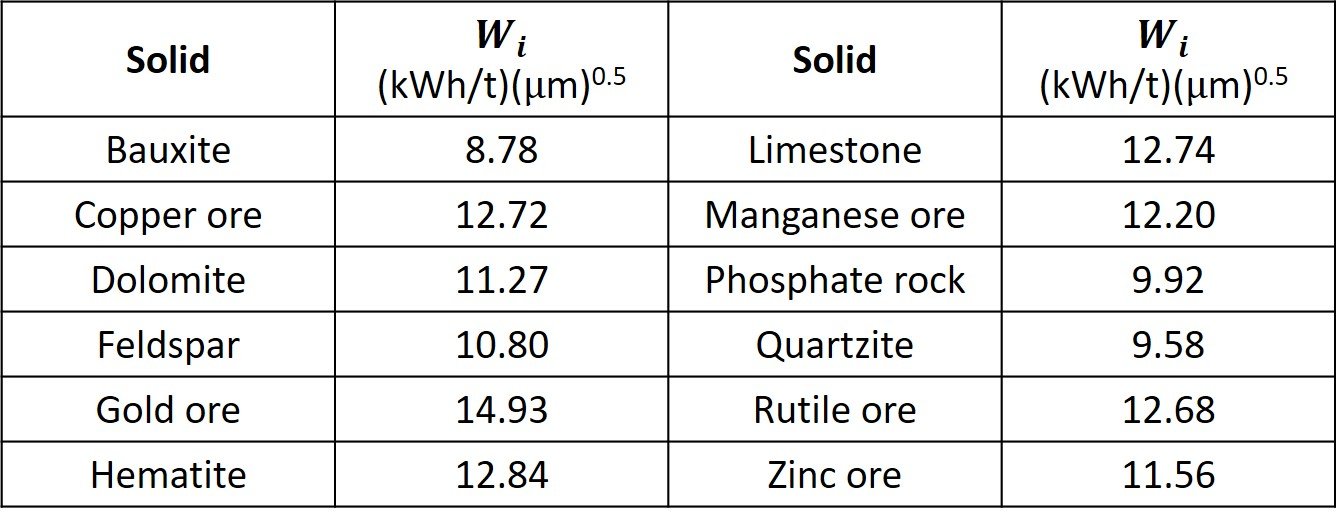
Note that the each of the three energy-based empirical correlations involve two constants: firstly, there is a proportionality constant K (i.e., KVR, KK, or KB), which refers to the crushing strength of the particles being subjected to breakage; secondly, there’s the exponent n, which indicates the region of the energy-particle size curve at which the comminution process takes place and specifies whether the grinding energy is roughly proportional to particle volume (n = 1, Kick equation), surface (n = 2, von Rittinger equation), or somewhere in between (n = 1.5, Bond equation).
According to Gupta and Yan (2016), it has been found that the von Rittinger equation is more applicable for coarse size reduction, while the Kick equation is more appropriate for finer size reductions in the region where large surface areas of particles are exposed as in the case of grinding operations. Bond’s intermediate value of 1.5 covers almost the entire range of particles encountered in ore processing practice.
In a review for a ASM publication, Morrell (in Anderson et al., 2014) notes that Bond’s contribution and what made his equation so successful is that he combined it with a series of associated laboratory tests for crushers, rod mills, and ball mills that, when applied to practical design situations, provided reasonably life-like responses, i.e., the methods actually worked. The fact that Bond’s approach remains widely used in industry nearly 70 years after the publication of the 1952 paper is a testament to the fact that he must have gotten it largely right. Experience has shown that, as applied to crushers, rod, and ball mills, his equations provide acceptable accuracy in design applications.
Interestingly, Bond never published any data to support the validity of his approach, though some authors did, especially between the late 1960s and early 1980s, and most concluded that his approach is fairly precise and reliable.
Bond’s approach covers conventional crushers, and rod and ball mills. However, in his day, autogenous grinding and semiautogenous grinding (AG/SAG) mills and high-pressure grinding rolls (HPGRs) were not common or not yet invented, and hence his approach does not explicitly encompass these machines. Proprietary techniques have adapted his equations for use with AG/SAG mills with varying degrees of accuracy.
We close this article with two simple examples.
Example 1 (Modified from Rao, 2016)
A crusher fed at the rate of 1 ton per hour is used to comminute cubes of 10-mm limestone to a product with size composition of 75% retained on 3-mm screen, 15% retained on 2-mm screen, and 10% retained on 1-mm screen. The crusher requires 12.5 kWh to carry out this operation. Determine the power required to crush 8-mm limestone cubes to 1.6 mm size with the same crusher being fed at the same rate using (A) the von Rittinger equation and (B) the Kick equation.
The first step is to determine the average product size on the first run,
Applying the von Rittinger equation a first time, we have
Applying the same equation to the second process, we have
Dividing (II) by (I) and solving for W gives
For a feed rate of 1.0 t/hr, the corresponding power is simply
Proceeding similarly with the Kick equation, we have, for the first run,
while, for the second process,
Dividing (IV) by (III) and solving for W yields
As before, for a feed rate of 1.0 t/hr, the corresponding power follows as
Example 2 (Modified from Rao, 2016)
A hematite ore was ground from a feed size of 80% passing 3.5 mesh to a product size of 80% passing 100 mesh for flotation treatment, and the power consumption in the process was verified to be 8.77 kWhr per ton of ore ground. Because of the changing nature of the ore with the increased depth of mining, the metallurgical recovery can only be maintained by finer grinding. Test work has indicated that by crushing the feed to 80% passing 5 mesh and grinding in a ball mill to 80% passing 400 mesh, recoveries will be satisfactory. Using the Bond equation, compute the energy required to grind two tons of this ore. Refer to the following table for mesh aperture sizes in micrometers.
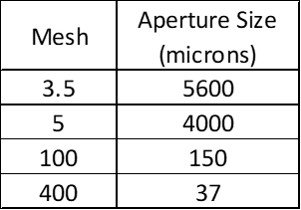
Substituting the data for the initial run gives
The Bond work index of the ore has been determined. (This result closely matches the reference value for hematite given in Table 1.) It remains to compute the work required for the second set of conditions,
The energy required to grind two tons of the ore in question is
References
• ANDERSON, C., DUNNE, R., and UHRIE, J. (Eds.) (2014). Mineral Processing and Extractive Metallurgy: 100 Years of Innovation. Littleton: Society for Mining, Metallurgy, and Exploration (SME).
• FEUERSTENAU, M. and HAN, K. (Eds.) (2003). Principles of Mineral Processing. Littleton: Society for Mining, Metallurgy, and Exploration (SME).
• GUPTA, A. and YAN, D. (2016). Mineral Processing Design and Operations: an Introduction. 2nd edition. Amsterdam: Elsevier.
• RAO, D. (2016). Minerals and Coal Process Calculations. Boca Raton: CRC Press.
• WILLS, B., and FINCH, J. (2016). Wills’ Mineral Processing Technology. 8th edition. Oxford: Butterworth-Heinemann.
