Shock Wave-Boundary Layer Interaction: Upstream and Downstream Mechanisms

1. Basics of shock wave-turbulent boundary layer interaction (SWBLI)

For over half a century, experimental and numerical research on the interaction between shock waves and turbulent boundary layers has been eagerly pursued by aerodynamicists around the world. Interaction between a shock and a separated flow constitutes one of the most elementary instances of viscous/inviscid interaction (Hadjadj and Dussauge, 2009).

The interaction of a shock wave with a boundary layer occurs in a variety of devices, including supersonic wind tunnel diffusers and high-speed intakes. Of particular interest are SWBLIs in supersonic intakes. These devices usually feature one or several compression ramps, forming a supersonic compression region through oblique SWBLIs. The supersonic compression region ends with a terminal shock, which during critical operation of the intake is located at the intake throat. The state of the boundary layer ahead of the terminal shock may lead to the formation of multiple SWBLIs in the intake throat.

The main characteristic of a typical SWBLI is that the shock motion usually has a frequency much lower than the characteristic frequency of the turbulent boundary layer. Such low-frequency unsteadiness leads to amplified wall pressure fluctuations accompanied by strong buffeting of the underlying structure; this entails intense mechanical loads and, at worst, culminates in fatigue-induced failure.

As a rule of thumb, for a boundary layer thickness  and a freestream velocity , the time scale associated with the shock motion is of the order O(10/ – 100/), in contrast to the characteristic time scale of the incoming boundary layer, which is O(/). The low-frequency motion manifests itself in the form of a separation ‘bubble’ accompanied by broadband movement of the reflected shock.

Touber and Sandham (2011) derived a model for the low-frequency unsteadiness by analyzing the momentum integral equation in the context of reflected shock interactions. Their model, which is reminiscent of an earlier approach adopted by Plotkin (1975), shows that the SWBLI behaves like a low-pass filter. External forcing is required to drive the model response. Physically, the required forcing may be provided by low-frequency content in either the incoming boundary layer or the separated flow downstream of the shock. This has led to two lines of thought to explain SWBLIs, namely a ‘upstream hypothesis’ and a ‘downstream hypothesis’, both of which we further discuss below.

Even though the sources of the separation shock motions are still under debate, recent research has suggested that the low-frequency unsteadiness of the separation shock is also fairly independent of the particular geometry of the flow (Dussauge et al., 2006). Some of the geometries that have been studied are shown in Figure 1; three common SWBLI settings are illustrated in Figure 2. Indeed, a dimensionless frequency of the separation shock oscillations can be defined which is readily shown to be almost constant for any shock-induced separation; this dimensionless frequency is the Strouhal number St,

where f is the characteristic shock motion frequency, L is the characteristic length of the interaction, and U is the velocity downstream of the separated shock. Many students will recall having ran into a problem that contains St while studying dimensional analysis in an elementary fluid mechanics course. Dussauge et al. (2006) surveyed SWBLI experiments covering a range of Mach and Reynolds numbers and including different geometries for generating the shock, such as compression ramps and three-dimensional fins. They found that in the supersonic regime, the central frequency of the unsteadiness typically lies in the Strouhal number range St = fL_sep/U_∞ = 0.02 – 0.05, where L_sep is the length of the separated flow and U_∞ is the freestream velocity. Souverein et al. (2013) developed a systematic treatment to define the interaction length L on the basis of experiments from various facilities at different configurations. In the same paper, Souverein’s team also accounted for Reynolds-number and Mach-number effects, finding that for turbulent boundary layers the onset of flow separation is nearly Reynolds number-independent. Rather, flow separation seems to be governed mainly by the Mach number and the imposed flow deflection angle – an increase in Mach number tends to reduce the deflection angle required for the onset of flow separation. In a later work, Jaunet et al. (2014) showed that the Souverein et al. (2013) interaction length scheme also applied to settings with wall heating, albeit with some modifications.

Figure 1. Canonical configurations employed for fundamental studies of SWBLI. (a) Impinging shock; (b) swept ramp; (c) double cone; (d) swept ramp; (e) single-fin; (f) double-fin; and (g) internal flowpath. From Gaitonde (2015).

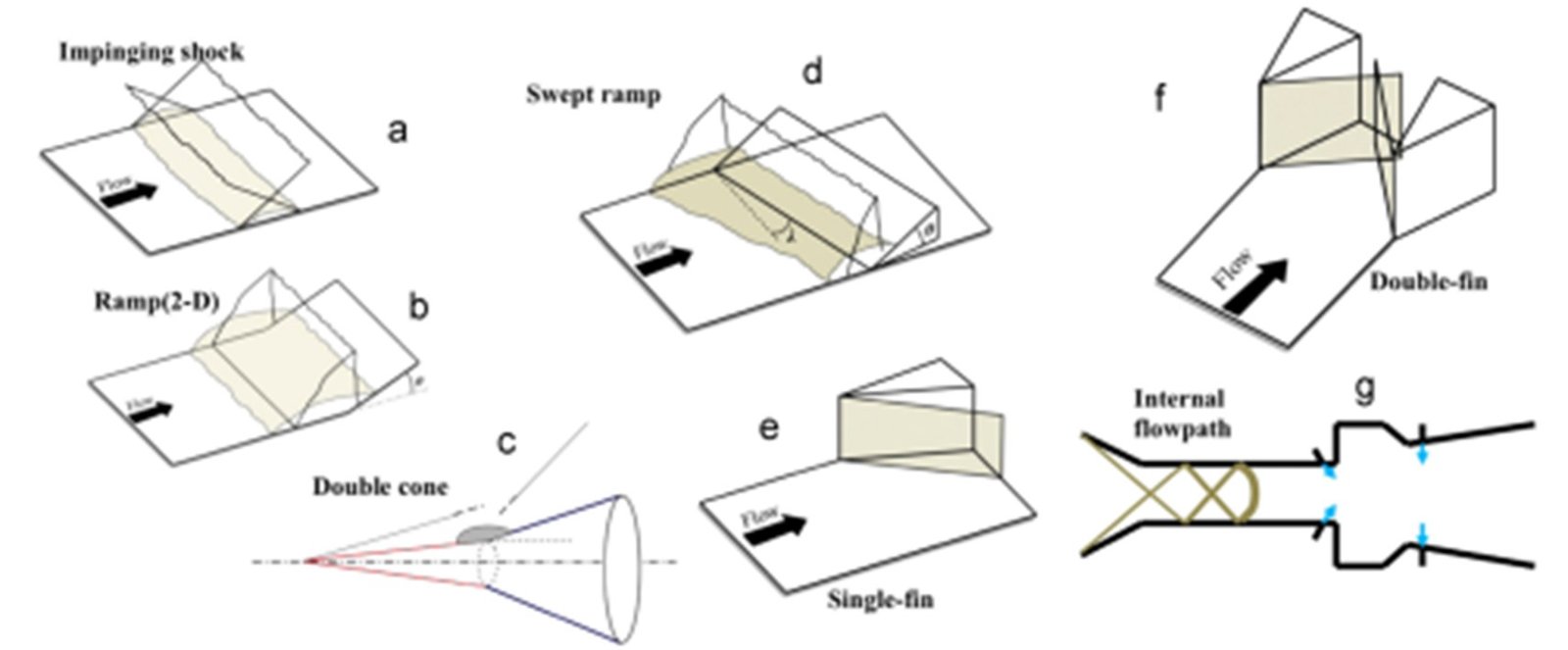
Figure 2. Schematic representation of typical situations in which SWBLI is encountered. Examples include (a) transonic shock-boundary layer separation; (b) oblique shock impinging turbulent boundary layer; and (c) supersonic flow over a compression ramp.

Of the cases illustrated in Figure 1, impinging SWBLI is probably the most popular in the research community. Still, very few numerical investigations for impinging SWBLI have encompassed sufficiently long integration times to capture low-frequency unsteadiness. Touber and Sandham (2009) is one of the few numerical studies to have achieved meaningful comparison between a long-time (in their case, 10⁴/U₀) narrow-domain LES and experimental data pertaining to the unsteady shock motion. Several such studies have been published in the years since, but most focused on weak interactions (with respect to the absence of a distinct pressure plateau within the separated flow) and low Reynolds numbers, typically Re  6010³. This is an important limitation because compression corner experiments (e.g., Dolling and Murphy, 1983; Dolling and Or, 1985) have shown that the wall-pressure signal near the separation-shock foot is highly intermittent and basically reflects the inviscid pressure jump across the oscillating shock (Pasquariello et al., 2017). For low Reynolds number studies, the reflected shock foot does not penetrate as deeply into the boundary layer as it does in the high Reynolds number case; increased viscous effects diffuse the separation-shock foot into a compression fan, which in turn results in a broader range of frequencies with attenuated shock intermittency.

Combs et al. (2019) studied SWBLI in a wind tunnel at NASA Langley Research Center. The flow was Mach 4.2 on the flat plate surface and Reynolds numbers varied from 710⁶ to 2610⁶. Figure 3 shows instantaneous Schlieren images of the shock interaction with the corresponding mean images of each experimental run. The images refer to different ranges of Reynolds number (ranging from Re = 710⁶ to 2310⁶) as indicated in the figure. The higher Reynolds number cases clearly display a shock interacting with an incoming turbulent boundary layer, as the turbulent boundary layer is visualized in the Schlieren images; the shock structure is reasonably well-defined both instantaneously and in the mean. Beginning with the Re_∞ = 1610⁶ case, the character of the interaction appears to change, as multiple forward shocks appear. For lower Reynolds numbers, the shock appears to be increasingly diffuse, and multiple, weaker shocks replace the single relatively strong shock observed when Re_∞ = 2310⁶.

Figure 3. Instantaneous (left) and mean (right) Schlieren visualizations of SWBLI as reported by Combs et al. (2019). The uppermost figure is a representative Schlieren image of a turbulent SWBLI.

Having presented a sample case study of SWBLI, we now turn to a discussion on the abovementioned hypotheses of low-frequency unsteadiness. Section 2 is devoted to the upstream hypothesis, while section 3 is devoted to the downstream hypothesis.

2. Upstream hypothesis

One of the first investigations of an upstream boundary layer mechanism for SWBLI unsteadiness is Andreopoulos and Muck (1987), who, working with Mach 3 flow along a compression ramp interaction, made wall-pressure measurements and established the time between shock crossings across a transducer within the intermittent region; the mean shock-crossing time period, T_m, was also computed. The shock zero-crossing frequency f_c = 1/T_m was found to correspond to a Strouhal number equal to 0.13, which Andreopoulos and his colleague took to be of the same order of magnitude as the bursting frequency of the upstream boundary layer (Clemens and Narayanaswamy, 2014). Those workers went on to note that, using T_m, they could infer the mean shock speed, which, they assumed, had the same order of magnitude as the upstream boundary layer bursting frequency, thereby lending credence to a possible upstream forcing mechanism. However, Dolling and Brusniak (1989) later contended that the single threshold technique adopted by Andreopoulos and Muck (1987) as a means to detect shock passage was susceptible to misinterpretation of turbulent fluctuations as shock passage motions; this meant that their zero-crossing frequencies were probably too high.

Later, Erengil and Dolling (1993) reported a direct response of the reflected shock to upstream pressure fluctuations, which however results in a high-frequency smaller-scale jitter motion that could not explain the large-scale low-frequency oscillations. Adams (2000) performed a direct numerical simulation (DNS) of a Mach 3 compression ramp flow and found the bursting frequency to be very close to the shock-crossing frequency, supporting the earlier experimental findings of Andreopoulos and Muck (1987).

More recently, Beresh et al. (2002) also noted that low-frequency shock motions can be inherited from the upstream boundary layer; specifically, Beresh’s team found a correlation between positive streamwise velocity fluctuations in the lower third of the upstream boundary layer and downstream shock motions. Later, using conditional analysis of experimental observations, Ganapathisubramani et al. (2007) were able to provide reasonable evidence for a statistical link between upstream large scales and unsteadiness. In their interpretation, the large-scale streaks observed in the outer turbulent wall layer, which become energetically significant at sufficiently high Reynolds number, and whose length can be much larger than the boundary layer thickness, would provide low-frequency undulation of the reflected shock foot, thus being responsible for the onset of very-low-frequency motions. From a system dynamics standpoint, the shock/separation bubble system could then be regarded as a low-pass filter capable of selectively amplifying the low-frequency motions in the upstream boundary layer.

Ganapathisubramani et al. (2009) observed a correlation between the shock motion and streamwise-elongated regions of low and high momentum in the incoming boundary layer. Those workers suggested that these large-scale boundary-layer structures, which are also known as superstructures, play a role in driving the low-frequency unsteadiness.

Pirozzoli and Grasso (2006) conducted a short-duration DNS of a Mach 2.25 impinging SWBLI and proposed an acoustic feedback mechanism as a possible driver of low-frequency unsteadiness. They assume that shear-layer vortices interacting with the incident-shock tip generate acoustic disturbances that propagate upstream through the subsonic layer while subsequently inducing an oscillatory motion of the separation point, similar to Rossiter modes in cavity flows. Touber and Sandham (2009) performed large-eddy simulations of the impinging SWLI experiment by Dupont et al. (2006) for a weak deflection angle of 8^o. Their linear-stability analysis of the mean flow revealed a two-dimensional, zero-frequency, globally unstable mode which could be linked to the low-frequency unsteadiness. Further, those workers detected upstream-travelling acoustic waves within the separation bubble, conferring evidence to the acoustic feedback mechanism proposed by Pirozzoli and Grasso (2006).

3. Downstream hypothesis

Theories of the second category relate the separation-shock motion to some mechanism originating from downstream of the shock. This line of thought stems from papers published in the early 1990s (e.g., Gramann and Dolling, 1990) in which workers, observing distinct correlations between pressure fluctuations in the upstream boundary layer and shock-foot unsteadiness, noted that downstream pressure fluctuations appeared to precede the shock-foot motion. Accordingly, some researchers went on to conclude that separated flow drives the interaction unsteadiness.

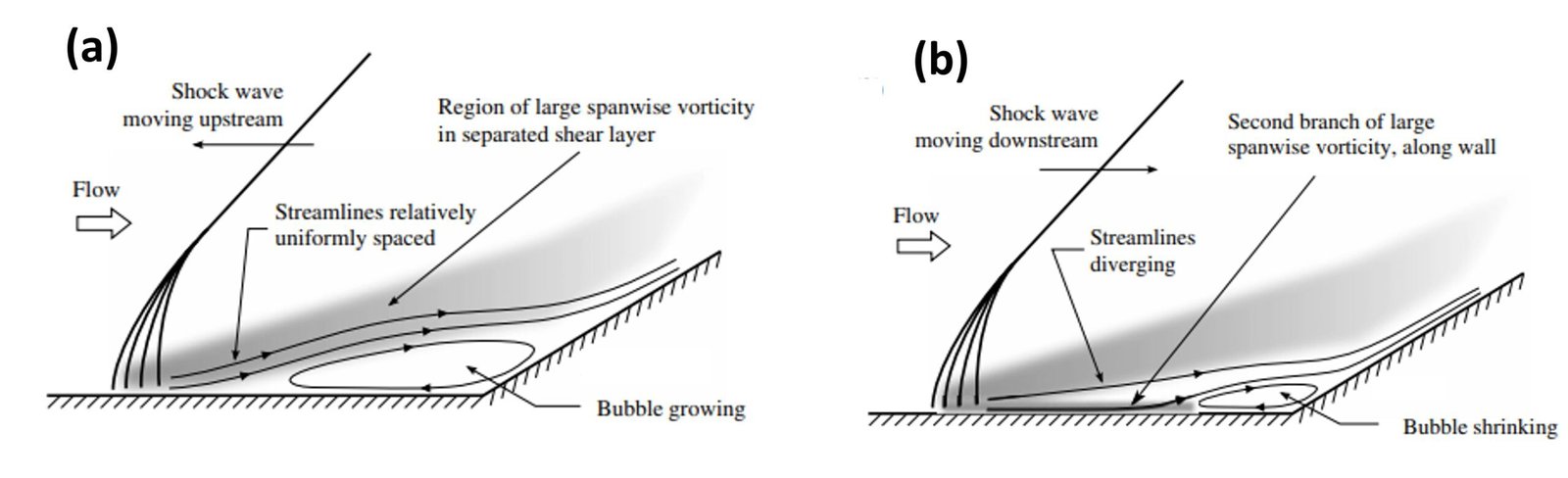
The downstream-driven mechanism traces back the reasons for observed energetic low-frequency motions to the relation between the dynamics of the separation bubble (when it is present) and the shock movements, either through intrinsic instability of the separation bubble or through some mechanism of dynamic self-sustainment of the shock/bubble system controlled by a feedback loop. In this vein, the low-frequency motion has been described by Priebe and Martín (2012) with a rather straightforward dynamics (Figure 4). First, they noted that the motion of the shock and the pulsation of the separation bubble are related. The growth of the bubble is associated with the shock moving upstream, whereas the shrinking of the bubble is associated with the shock moving downstream. The structure of the separated shear layer changes depending on the phase of the low-frequency motion. As the bubble grows, a single branch of strong vorticity exists downstream of the separation, making an angle with the wall and lying above the recirculation bubble. The shear layer velocity profiles are akin to those of a plane mixing layer with a single inflection point. As the bubble shrinks, the vorticity field downstream of the separation has a bifurcation with a second branch of strong vorticity along the wall where the flow is reattaching; then, the bubble breaks. Priebe and Martín thus conclude that the low-frequency pulsations of the downstream separated flow involve changes in flow structure and not just changes in the flow field length scale.

Figure 4. Schematics of the different flow structures observed depending on the phase of low-frequency motion: (a) bubble growth phase; and (b) bubble collapse phase. 

The downstream hypothesis has been supported in experimental work by Erengil and Dolling (1991), based on compression ramp configurations, and, more recently, by Dupont et al. (2006), based on impinging SWBLI. These studies showed that wall-pressure fluctuations measured close to the shock foot and near reattachment are correlated at frequencies connected to the separation-shock motion. The measured phase shift indicates that the separation bubble expands and contracts periodically, as noted above. Similarly, based on conditionally-averaged particle image velocimetry (PIV) velocity fields for small and large bubbles, Piponniau et al. (2009) found that the position of the reflected shock is located more downstream and upstream, respectively. Piponniau’s team attempted to explain low-frequency shock motions through a self-sustaining mechanism based on fluid entrainment by the shear layer generated downstream of the reflected shock above the closed separation bubble.

Wu and Martin (2008) used DNS data in a SWBLI study of their own. Employing a compression-ramp configuration, those workers found that upstream boundary layer structures cause smaller-scale unsteadiness, whereas large-scale motion is driven by pulsations of the separated flow. They argued that pulsations may be driven by an instability that is similar to the wake flow instability that characterizes cavity flows. They further argued that the shear layer may flap in response to an imbalance in (1) the entrainment rate of the shear layer, and (2) the separation bubble recharge rate near reattachment. Wu and Martin’s (2008) model is quite similar to the mechanism proposed by Piponniau et al. (2009), as it is based on an entrainment/recharge mechanism of the separated shear layer.

In summary, separated flow undergoes breathing motions or pulsations, and much attention has been devoted to the role of the separated flow, downstream of the shock, as a possible source of low-frequency unsteadiness. The pulsations have been detected in several instances, including experimental work and numerical models. Still, Martín et al. (2016) caution that the fact that the separated flow pulsates could reveal little about the physical mechanism of the SWBLI unsteadiness, in that it may be caused by low-frequency disturbances in the incoming boundary layer convecting through the interaction.

4. Reconciling the hypotheses

As mentioned by Waindim et al. (2020), understanding the cause of low-frequency unsteadiness in SWBLI is not merely a theoretical issue, because it has important implications for practical aerodynamics. For instance, if the superstructures in the upstream turbulence are necessary for the unsteadiness in the interaction, control applications could focus on breaking them up or inhibiting their formation. Alternatively, if the unsteadiness arises from the interaction itself, an effective control mechanism may target the separation bubble driving the shock motion or rely on manipulation of the shear-layer entrainment characteristics.

Priebe and Martín (2012), who had subscribed to the downstream hypothesis, attempted to reconcile their findings with those of Ganapathisubramani et al. (2007, 2009) and Humble et al. (2012), who had concluded that the incoming boundary layer is at the origin of the low-frequency unsteadiness. Priebe and his colleague argue that those investigators worked with weakly separated regions, for which upstream perturbations may be particularly important. Simply put, it may be the case that the relative importance of the low-frequency dynamics of the separated flow as compared to the importance of the upstream flow is dependent on the degree of separation and hence the interaction strength. In this view, suggested for example in Clemens and Narayanaswamy (2009) and Souverein et al. (2010), both upstream and downstream effects are always present, but their relative importance is dependent on aerodynamic conditions. Downstream effects appear to dominate for fully separated cases, whereas upstream effects are expected to become relatively more important for mild interactions.

References

Download references list here.